/Szkoła średnia

Zadanie nr 9830477

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 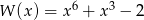6 3 W (x) = x + x − 2 jest równy iloczynowi
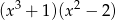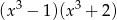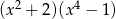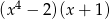
A) (x3 + 1)(x2 − 2) B) (x 3 − 1 )(x3 + 2) C) (x2 + 2)(x4 − 1) D) (x4 − 2)(x + 1 )

Rozwiązanie

Sposób I

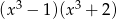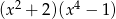Patrzymy na podane odpowiedzi, wielomian stopnia 6 otrzymamy tylko w przypadku odpowiedzi: (x 3 − 1)(x 3 + 2 ) lub (x2 + 2)(x4 − 1) . Sprawdzamy, która z nich jest poprawna

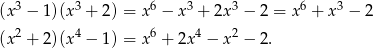
(x 3 − 1 )(x3 + 2) = x6 − x3 + 2x3 − 2 = x 6 + x 3 − 2 2 4 6 4 2 (x + 2 )(x − 1) = x + 2x − x − 2.

Sposób II

Podstawiając 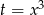t = x3 otrzymujemy funkcję kwadratową, wyznaczamy jej pierwiastki

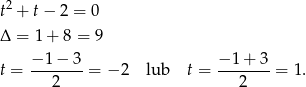
2 t + t− 2 = 0 Δ = 1+ 8 = 9 − 1 − 3 − 1+ 3 t = ------- = − 2 lub t = ------- = 1. 2 2

Zatem

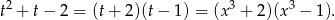
2 3 3 t + t− 2 = (t + 2)(t− 1) = (x + 2)(x − 1).

 
Odpowiedź: B

Wersja PDF