/Szkoła średnia

Zadanie nr 9833138

Dodaj do ulubionych
Dodaj do rozwiązanych

Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.

Rozwiązanie

Sposób I

Jeżeli za zdarzenia elementarne przyjmiemy uporządkowane trójki 3 monet, to wszystkich zdarzeń elementarnych jest

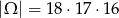
|Ω | = 18 ⋅17 ⋅16

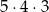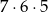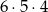(pierwszą monetę możemy wybrać na 18 sposobów, drugą na 17, a trzecią na 16). Zdarzenia sprzyjające są trzech rodzajów – mogą to być 3 jedynki, dwójki lub piątki. W przypadku 3 jedynek, mamy 5⋅ 4⋅3 zdarzeń sprzyjających (pierwszą możemy wybrać na 5 sposobów, drugą na 4, trzecią na 3). Podobnie w pozostałych przypadkach mamy odpowiednio 7 ⋅6 ⋅5 i 6⋅ 5⋅4 możliwości. Zatem szukane prawdopodobieństwo jest równe

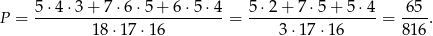
P = 5-⋅4-⋅3+--7⋅6-⋅5-+-6-⋅5⋅-4 = 5-⋅2-+-7-⋅5+--5⋅-4 = -65-. 18 ⋅17 ⋅16 3⋅17 ⋅16 81 6

Sposób II

Tym razem za zdarzenia elementarne przyjmijmy nieuporządkowane zbiory trzech wylosowanych monet. Zatem

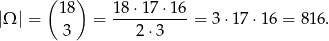
( ) |Ω | = 18 = 18-⋅17-⋅16-= 3⋅17 ⋅16 = 816. 3 2 ⋅3

Tak jak poprzednio zdarzenia sprzyjające są trzech rodzajów i jest ich

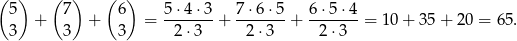
( ) ( ) ( ) 5 7 6 5-⋅4-⋅3 7-⋅6⋅-5 6-⋅5⋅-4 3 + 3 + 3 = 2⋅3 + 2⋅3 + 2 ⋅3 = 10 + 35 + 20 = 65.

Zatem

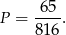
65 P = ----. 81 6

 
Odpowiedź: 65 816

Wersja PDF