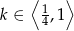/Szkoła średnia

Zadanie nr 9834832

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 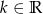k ∈ R równanie 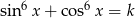6 6 sin x + cos x = k ma rozwiązanie?

Rozwiązanie

Zauważmy, że

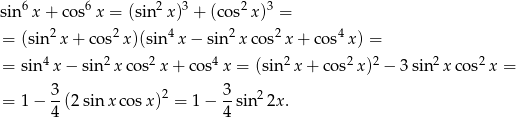
6 6 2 3 2 3 sin x + co s x = (sin x) + (cos x) = = (sin 2x + cos2 x)(sin 4x − sin2 xcos2 x+ cos4x ) = 4 2 2 4 2 2 2 2 2 = sin x − sin x cos x+ cos x = (sin x + cos x) − 3sin x cos x = 3 2 3 2 = 1− --(2sinx cos x) = 1 − --sin 2x . 4 4

Dane równanie możemy więc zapisać w postaci

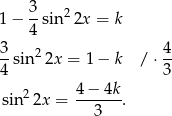
3 1 − --sin22x = k 4 3- 2 4- 4 sin 2x = 1 − k / ⋅ 3 4− 4k sin2 2x = ------. 3

To równanie ma rozwiązanie wtedy i tylko wtedy, gdy prawa strona jest liczbą z przedziału 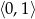⟨0 ,1⟩ (takie wartości może przyjmować plewa strona), tzn. gdy

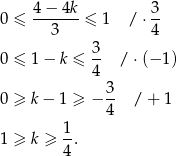
4 − 4k 3 0 ≤ -------≤ 1 / ⋅ -- 3 4 0 ≤ 1 − k ≤ 3- / ⋅(− 1) 4 3- 0 ≥ k − 1 ≥ − 4 / + 1 1 1 ≥ k ≥ --. 4

 
Odpowiedź: ⟨ ⟩ k ∈ 14,1

Wersja PDF