/Szkoła średnia

Zadanie nr 9849653

Dodaj do ulubionych
Dodaj do rozwiązanych

Kule o jednakowych promieniach ułożono w rzędach tworząc w ten sposób kwadrat. Gdyby usunięto 669 kul, to z pozostałych można by było zbudować trójkąt równoboczny (w pierwszym rzędzie jedna kula, w drugim dwie, w trzecim trzy itd.) Bok trójkąta równobocznego zawierałby wówczas o 8 kul więcej niż bok kwadratu. Z ilu kul zbudowany był kwadrat?

Rozwiązanie

Powiedzmy, że na początku kwadrat był zbudowany z 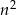2 n kul. Zatem trójkąt równoboczny zbudowano z 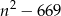n2 − 669 kul. Wiemy ponadto, że na boku trójkąta było 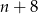n + 8 kul, czyli dokładnie tyle było rzędów, w których ułożono kuli.

PIC

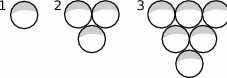
Możemy zatem policzyć liczbę kul w trójkącie ze wzoru na sumę kolejnych wyrazów ciągu arytmetycznego.

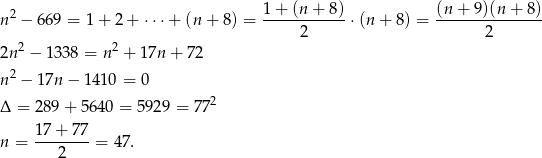
2 1+--(n+--8)- (n-+--9)(n+--8) n − 669 = 1+ 2 + ⋅ ⋅⋅+ (n + 8) = 2 ⋅(n + 8) = 2 2n2 − 1338 = n2 + 17n + 72 n2 − 17n − 14 10 = 0 2 Δ = 289+ 5640 = 5929 = 77 17+--77- n = 2 = 47 .

Zatem początkowo było 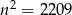2 n = 22 09 kul.  
Odpowiedź: 2209 kul.

Wersja PDF