Zadanie nr 9850067
Wiadomo, że 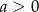 i
i 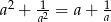 . Wykaż, że
. Wykaż, że 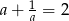 .
.
Rozwiązanie
Niech 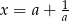 . Wtedy
. Wtedy 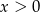 oraz
oraz
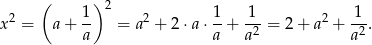
W takim razie daną równość możemy zapisać w postaci
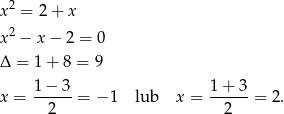
Ponieważ 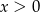 , mamy stąd
, mamy stąd 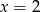 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiadomo, że 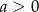 i
i 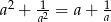 . Wykaż, że
. Wykaż, że 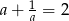 .
.
Niech 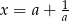 . Wtedy
. Wtedy 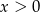 oraz
oraz
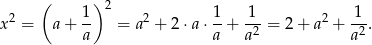
W takim razie daną równość możemy zapisać w postaci
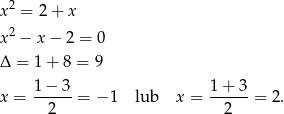
Ponieważ 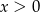 , mamy stąd
, mamy stąd 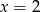 .
.
