/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 15 kwietnia 2023 Czas pracy: 180 minut
Ciąg 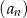 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 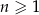 wzorem
wzorem
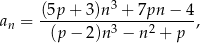
gdzie 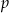 jest liczbą rzeczywistą. Oblicz wartość
jest liczbą rzeczywistą. Oblicz wartość 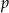 , dla której granica ciągu
, dla której granica ciągu 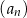 jest równa
jest równa 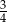 .
.
W firmie zatrudniającej 390 pracowników sporządzono zestawienie wszystkich pracowników w wieku przedemerytalnym i okazało się, że wśród nich jest 96 mężczyzn i 45 kobiet. Prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany mężczyzna pracujący w tej firmie jest w wieku przedemerytalnym jest równe 0,4. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej firmy jest w wieku przedemerytalnym – pod warunkiem, że jest to kobieta.
Funkcja 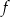 jest określona wzorem
jest określona wzorem 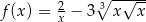 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 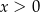 . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 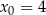 .
.
Wykaż, że dla każdej liczby rzeczywistej  oraz dla każdej liczby rzeczywistej
oraz dla każdej liczby rzeczywistej 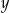 , spełniających warunek
, spełniających warunek 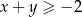 , prawdziwa jest nierówność
, prawdziwa jest nierówność
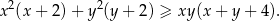
Iloczyn wszystkich wyrazów ciągu danego wzorem
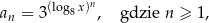
jest równy 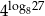 . Oblicz
. Oblicz  .
.
W trójkącie 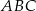 na boku
na boku 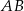 wybrano takie punkty
wybrano takie punkty 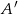 i
i 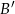 , że
, że
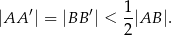
Przez punkty 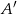 i
i 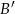 poprowadzono proste równoległe do boków odpowiednio
poprowadzono proste równoległe do boków odpowiednio 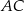 i
i 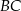 . Proste te przecięły się w punkcie
. Proste te przecięły się w punkcie 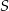 . Wykaż, że odcinek
. Wykaż, że odcinek 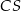 jest zawarty w środkowej trójkąta
jest zawarty w środkowej trójkąta 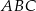 .
.
Rozwiąż równanie 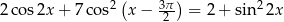 w przedziale
w przedziale ![[0 ,2π]](https://img.zadania.info/zes/0098530/HzesT31x.gif) .
.
Informacja do zadań 8.1 i 8.2
W parku krajobrazowym znajduje się zbiornik wodny, którego dwa brzegi postanowiono połączyć pomostem. Na podstawie dostępnych map wymodelowano w pewnej skali kształt linii brzegowej zbiornika w kartezjańskim układzie współrzędnych 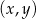 za pomocą fragmentów wykresów funkcji
za pomocą fragmentów wykresów funkcji 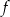 oraz
oraz 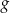 , które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
, które odpowiadają przeciwległym brzegom zbiornika (zobacz rysunek).
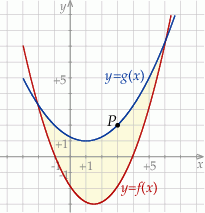
Funkcje  oraz
oraz  są określone wzorami
są określone wzorami 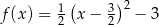 oraz
oraz 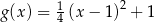 . Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją
. Jeden z końców pomostu postanowiono zlokalizować na brzegu opisanym funkcją 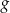 w punkcie o współrzędnych
w punkcie o współrzędnych 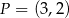 .
.
Niech 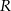 będzie punktem leżącym na wykresie
będzie punktem leżącym na wykresie 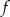 . Wykaż, że odległość punktu
. Wykaż, że odległość punktu 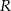 od punktu
od punktu 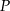 wyraża się wzorem
wyraża się wzorem
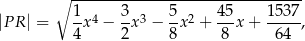
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 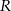 .
.
Koniec pomostu należy umieścić na brzegu opisanym funkcją 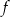 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 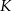 , w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca
, w którym należy zlokalizować koniec pomostu, aby jego długość (tj. odległość końca 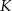 pomostu od początku
pomostu od początku 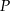 ) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
) była możliwie najmniejsza. Oblicz długość najkrótszego pomostu.
Przy rozwiązywaniu zadania możesz skorzystać z tego, że odległość dowolnego punktu 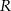 leżącego na wykresie funkcji
leżącego na wykresie funkcji 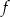 od punktu
od punktu 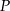 wyraża się wzorem
wyraża się wzorem
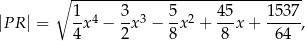
gdzie  jest pierwszą współrzędną punktu
jest pierwszą współrzędną punktu 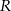 .
.
Dany jest ostrosłup prawidłowy trójkątny 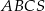 o podstawie
o podstawie 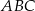 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym 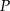 . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 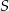 ma miarę
ma miarę 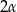 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 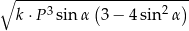 , gdzie
, gdzie 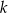 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 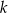 .
.
Rozwiąż nierówność
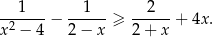
Dany jest równoległobok, którego boki zawierają się w prostych o równaniach: 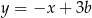 ,
, 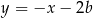 ,
, 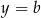 ,
, 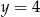 , gdzie liczba rzeczywista
, gdzie liczba rzeczywista 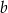 spełnia warunki:
spełnia warunki: 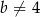 i
i 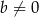 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 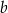 , dla których pole tego równoległoboku jest równe 20.
, dla których pole tego równoległoboku jest równe 20.
W okrąg o średnicy 16,25 wpisano trójkąt ostrokątny 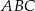 , w którym
, w którym 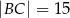 . Miary kątów
. Miary kątów 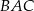 i
i 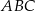 tego trójkąta spełniają warunek
tego trójkąta spełniają warunek
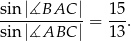
Oblicz promień okręgu wpisanego w trójkąt 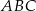 .
.

