Zadanie nr 9859199
Rzucamy 5 razy symetryczną monetą. Oblicz prawdopodobieństwo otrzymania co najmniej 4 orłów lub co najmniej 4 reszek, jeżeli wiadomo, że otrzymaliśmy co najmniej jedną reszkę.
Rozwiązanie
Sposób I
Założenie o tym, że otrzymaliśmy co najmniej jedną reszkę oznacza, że za zdarzenia elementarne możemy przyjąć ciągi otrzymanych reszek/orłów i możemy założyć, że nie ma wśród nich ciągu 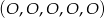 . Jest więc
. Jest więc
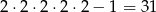
zdarzeń elementarnych.
Zamiast obliczać ile jest zdarzeń sprzyjających obliczmy, ile jest zdarzeń przeciwnych. W zdarzeniach tych otrzymaliśmy 3 orły i 2 reszki lub odwrotnie. Ze względu na symetryczną rolę reszek i orłów, będzie dokładnie tyle samo zdarzeń sprzyjających w obu przypadkach, więc zajmiemy się tylko sytuacją z 3 orłami i 2 reszkami. Miejsca dla reszek możemy wybrać na
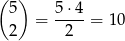
sposobów, a na pozostałych miejscach musimy umieścić orły. Jest więc 20 zdarzeń, w których nie mamy co najmniej 4 orłów lub co najmniej 4 reszek. Interesujące nas prawdopodobieństwo jest wiec równe
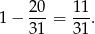
Sposób II
Jeżeli oznaczymy przez 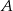 zdarzenie polegające na otrzymaniu co najmniej 4 orłów lub co najmniej 4 reszek, a przez
zdarzenie polegające na otrzymaniu co najmniej 4 orłów lub co najmniej 4 reszek, a przez 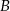 zdarzenie polegające na otrzymaniu co najmniej 1 reszki, to musimy obliczyć
zdarzenie polegające na otrzymaniu co najmniej 1 reszki, to musimy obliczyć
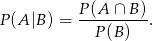
Jest tylko jedno zdarzenie przeciwne do 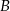 – jest to zdarzenie, w którym otrzymaliśmy same orły, więc
– jest to zdarzenie, w którym otrzymaliśmy same orły, więc
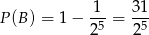
(bo wszystkich możliwych wyników pięciokrotnego rzutu monetą jest 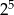 ).
).
Zajmijmy się teraz zdarzeniem 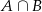 . Łatwo wypisać wszystkie zdarzenia sprzyjające temu zdarzeniu:
. Łatwo wypisać wszystkie zdarzenia sprzyjające temu zdarzeniu:
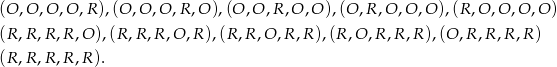
Interesujące nas prawdopodobieństwo jest więc równe
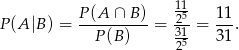
Odpowiedź: