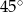/Szkoła średnia

Zadanie nr 9859404

Dodaj do ulubionych
Dodaj do rozwiązanych

Dane są dwie bryły: stożek, w którym długość promienia podstawy jest równa 2 dm i wysokość ma długość 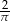2π- dm oraz ostrosłup prawidłowy trójkątny, w którym krawędź podstawy ma długość 4 dm. Wiedząc, że objętości tych brył są równe, wyznacz kąt nachylenia ściany bocznej ostrosłupa do jego podstawy.

Rozwiązanie

Możemy sobie naszkicować obie bryły.

PIC

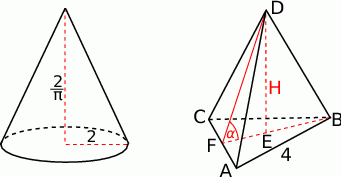
Porównujemy ich objętości.

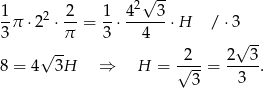
2√ -- 1-π ⋅22 ⋅ 2-= 1-⋅ 4--3-⋅H /⋅ 3 3 π 3 4 √ -- 2 2√ 3- 8 = 4 3H ⇒ H = √---= ----. 3 3

Teraz z trójkąta 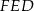FED wyliczymy tangens szukanego kąta α nachylenia ściany bocznej do podstawy.

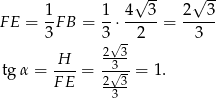
√ -- √ -- 1- 1- 4--3- 2--3- F E = 3 FB = 3 ⋅ 2 = 3 2√ 3 H-- --3- tg α = FE = 2√-3 = 1. 3

W takim razie 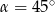∘ α = 45 .  
Odpowiedź: 45∘

Wersja PDF