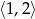/Szkoła średnia

Zadanie nr 9862332

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż algebraicznie i graficznie nierówność 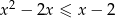2 x − 2x ≤ x− 2 , gdzie x ∈ R .

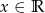Rozwiązanie

Rysujemy wykresy obu stron nierówności.

PIC

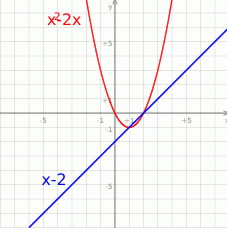
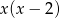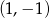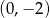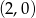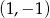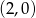Parabola x(x − 2 ) z lewej strony ma miejsca zerowe w 0 i 2, oraz wierzchołek w punkcie (1 ,−1 ) . Wykresem prawej strony jest prosta przechodząca przez punkty (0,− 2) i (2,0 ) . Punkty wspólne tych wykresów to (1,− 1) i (2,0) , co daje nam rozwiązanie nierówności: ⟨1,2⟩ .

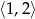Teraz rozwiążmy nierówność algebraicznie.

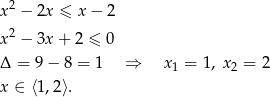
2 x − 2x ≤ x − 2 x2 − 3x+ 2 ≤ 0 Δ = 9 − 8 = 1 ⇒ x1 = 1, x2 = 2 x ∈ ⟨1,2⟩.

 
Odpowiedź: ⟨1,2⟩

Wersja PDF