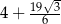Zadanie nr 9868456
Kąt 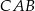 trójkąta prostokątnego
trójkąta prostokątnego 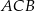 ma miarę
ma miarę 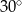 . Pole kwadratu
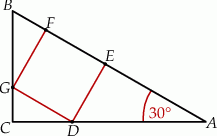
. Pole kwadratu 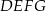 , wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta
, wpisanego w ten trójkąt (zobacz rysunek), jest równe 4. Oblicz pole trójkąta 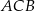 .
.
Rozwiązanie
Oczywiście bok kwadratu 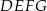 to 2. Zauważmy teraz, że w każdym z trójkątów prostokątnych
to 2. Zauważmy teraz, że w każdym z trójkątów prostokątnych 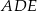 ,
, 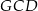 ,
, 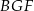 jeden z kątów ostrych ma miarę
jeden z kątów ostrych ma miarę 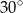 oraz jeden z boków ma długość 2. To pozwala dość łatwo obliczyć długości przyprostokątnych trójkąta.
oraz jeden z boków ma długość 2. To pozwala dość łatwo obliczyć długości przyprostokątnych trójkąta.
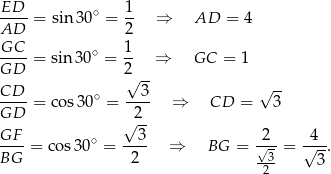
W takim razie
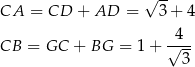
i pole trójkąta  jest równe
jest równe
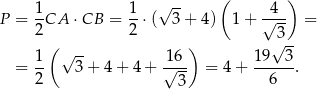
Odpowiedź: