/Szkoła średnia

Zadanie nr 9873099

Dodaj do ulubionych
Dodaj do rozwiązanych

W prostokącie połączono środki sąsiednich boków. Powstały w ten sposób romb ma obwód 40 cm i pole równe 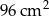9 6 cm 2 . Oblicz długości boków prostokąta.

Rozwiązanie

Zaczynamy od rysunku.

PIC

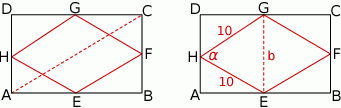
Oznaczmy szukane długości boków prostokąta przez a i b .

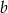Sposób I

Ponieważ odcinek 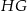HG łączy środki boków w trójkącie 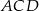ACD , ma on długość (twierdzenie Talesa) równą połowie przekątnej prostokąta (tak samo jest z innymi bokami czworokąta 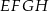EF GH – dlatego jest to romb). Przekątna prostokąta ma długość 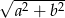√ ------- a2 + b2 i z podanego obwodu rombu mamy

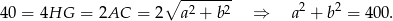
∘ ------- 40 = 4HG = 2AC = 2 a2 + b2 ⇒ a2 + b2 = 400.

Pole rombu możemy policzyć ze wzoru z przekątnymi:

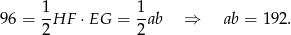
1- 1- 96 = 2HF ⋅EG = 2ab ⇒ ab = 192.

Mamy zatem układ równań

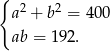
{ a2 + b2 = 400 ab = 1 92.

Przekształćmy pierwsze równanie tak aby pozbyć się kwadratów.

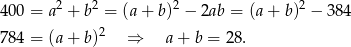
2 2 2 2 400 = a + b = (a+ b ) − 2ab = (a+ b) − 384 784 = (a + b )2 ⇒ a+ b = 28.

Podstawmy teraz 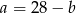a = 28 − b do drugiego równania.

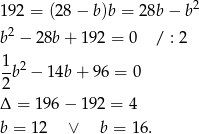
19 2 = (28 − b)b = 2 8b− b2 2 b − 28b + 1 92 = 0 / : 2 1 2 -b − 14b + 96 = 0 2 Δ = 196 − 19 2 = 4 b = 12 ∨ b = 16 .

Wtedy odpowiednio 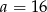a = 16 lub a = 12 .

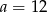Sposób II

Oznaczmy miarę kąta ostrego rombu przez α . Z podanego pola rombu mamy więc

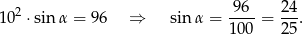
102 ⋅sinα = 96 ⇒ sin α = 96--= 24. 100 25

Z jedynki trygonometrycznej obliczamy 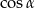cos α .

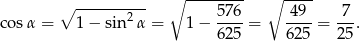
∘ ---------- ∘ -------- ∘ ---- co sα = 1− sin 2α = 1− 576-= -49- = -7-. 625 6 25 2 5

Teraz z twierdzenia cosinusów w trójkącie 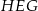HEG obliczamy b = GE .

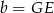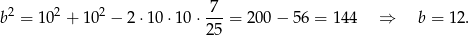
7 b2 = 102 + 102 − 2 ⋅10 ⋅10 ⋅---= 200 − 56 = 14 4 ⇒ b = 12. 25

Drugi bok prostokąta obliczamy z trójkąta prostokątnego DHG .

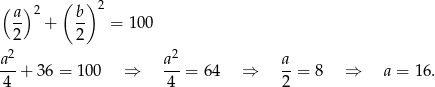
( ) ( ) 2 a- 2 b- 2 + 2 = 100 2 2 a--+ 3 6 = 100 ⇒ a--= 64 ⇒ a-= 8 ⇒ a = 16. 4 4 2

 
Odpowiedź: 12 cm i 16 cm

Wersja PDF