/Szkoła średnia

Zadanie nr 9877506

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz sumę kwadratów pierwiastków równania 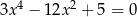4 2 3x − 12x + 5 = 0 .

Rozwiązanie

Podstawmy 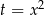2 t = x w danym równaniu

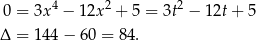
4 2 2 0 = 3x − 12x + 5 = 3t − 12t+ 5 Δ = 144 − 60 = 84.

Równanie to ma więc dwa rozwiązania 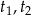t1,t2 , które w dodatku są dodatnie, bo na mocy wzorów Viète’a

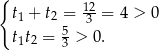
{ t + t = 12 = 4 > 0 1 25 3 t1t2 = 3 > 0.

Oryginalne równanie ma więc cztery pierwiastki: 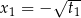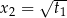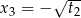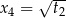√ -- x1 = − t1 , √ -- x2 = t1 , x = − √t-- 3 2 , x = √t-- 4 2 . Ich suma kwadratów jest równa

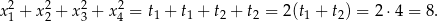
x2+ x2+ x2+ x2 = t + t + t + t = 2(t + t ) = 2 ⋅4 = 8 . 1 2 3 4 1 1 2 2 1 2

 
Odpowiedź: 8

Wersja PDF