Zadanie nr 9889543

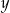Wykaż, że dla każdej dodatniej liczby rzeczywistej różnej od 1 oraz dla każdej dodatniej liczby rzeczywistej różnej od 1 prawdziwa jest równość

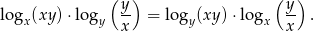
( y) ( y) logx (xy) ⋅lo gy -- = logy(xy )⋅logx -- . x x

Rozwiązanie

Sposób I

Przekształcamy daną tożsamość w sposób równoważny – korzystamy ze wzorów na logarytm iloczynu i ilorazu.

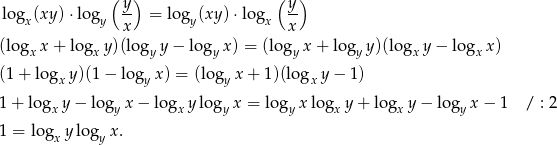
( ) ( ) log (xy )⋅log y- = lo g (xy) ⋅log y- x y x y x x (lo g x + log y)(log y− lo g x ) = (lo g x + log y)(log y− lo g x ) x x y y y y x x (1+ lo gxy )(1− logy x) = (logy x + 1)(logx y− 1) 1+ lo gxy − logy x − logx ylogy x = logy xlogx y + logx y− logy x − 1 / : 2 1 = log ylog x. x y

Aby uzasadnić powyższą równość, korzystamy ze wzoru na zmianę podstawy logarytmu.

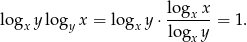
logxx logx ylogy x = logx y⋅ ------ = 1. logx y

Sposób II

Przekształcamy daną tożsamość w sposób równoważny – zmieniamy podstawy wszystkich logarytmów na .

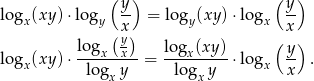
( ) ( ) lo g (xy) ⋅log y- = log (xy )⋅log y- x y (x) y x x log y log (xy ) ( y) lo gx(xy) ⋅---x--x--= ---x-----⋅ logx -- . logx y logx y x

Otrzymana równość jest oczywiście spełniona, więc wyjściowa równość też musiała być prawdziwa.