Zadanie nr 9902082
Dany jest trójkąt 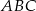 , w którym
, w którym 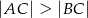 . Na bokach
. Na bokach 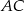 i
i 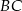 tego trójkąta obrano odpowiednio takie punkty
tego trójkąta obrano odpowiednio takie punkty 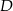 i
i 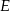 , że
, że 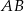 i
i 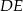 przecinają się w punkcie
przecinają się w punkcie 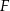 (zobacz rysunek). Wykaż, że jeżeli
(zobacz rysunek). Wykaż, że jeżeli 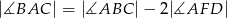 , to
, to 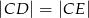 .
.
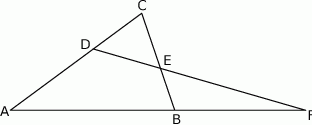
Rozwiązanie
Oznaczmy 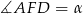 i
i 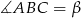 .
.
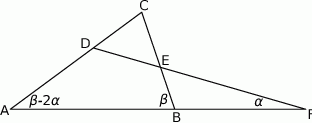
Z założenia 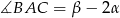 , więc w trójkącie
, więc w trójkącie 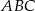 mamy
mamy
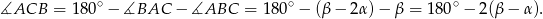
Teraz patrzymy na trójkąt 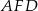 .
.
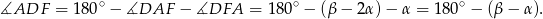
Teraz patrzymy na trójkąt 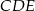 .
.
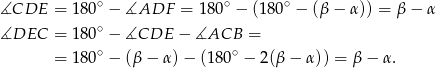
To oznacza, że trójkąt 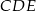 jest równoramienny i rzeczywiście
jest równoramienny i rzeczywiście 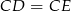 .
.

