Zadanie nr 9915079
Przyprostokątne trójkąta prostokątnego 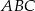 mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek
mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek 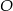 leży na przeciwprostokątnej, oraz oblicz odległości środka
leży na przeciwprostokątnej, oraz oblicz odległości środka 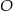 od wierzchołków trójkąta
od wierzchołków trójkąta 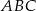 .
.
Rozwiązanie
Zacznijmy od rysunku.
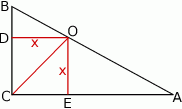
Sposób I
Ponieważ środek 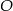 jest odległy o tyle samo od boków
jest odległy o tyle samo od boków 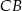 i
i 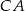 , to prosta
, to prosta 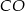 jest dwusieczną kąta
jest dwusieczną kąta 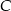 . Zatem z twierdzenia o dwusiecznej mamy
. Zatem z twierdzenia o dwusiecznej mamy
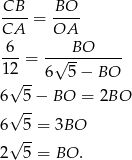
Stąd 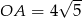 . Aby wyliczyć promień
. Aby wyliczyć promień 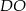 okręgu, korzystamy z podobieństwa trójkątów
okręgu, korzystamy z podobieństwa trójkątów 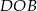 i
i 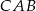 .
.
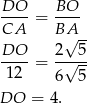
Pozostało obliczyć długość odcinka 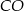 . Ponieważ jest to przekątna w kwadracie
. Ponieważ jest to przekątna w kwadracie 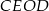 , więc
, więc
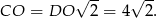
Sposób II
Tym razem od razu skorzystajmy z podobieństwa trójkątów 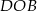 i
i 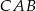 .
.
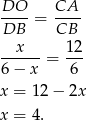
Dalej
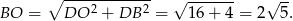
Stąd 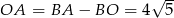 oraz
oraz 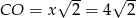 .
.
Odpowiedź: Promień: 4, odległości: 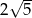 ,
, 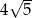 i
i