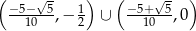/Szkoła średnia

Zadanie nr 9916119

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest wielomian 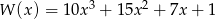3 2 W (x) = 10x + 15x + 7x + 1 .

  • Zapisz wielomian 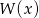W (x) jako iloczyn wielomianów liniowych.
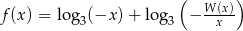  • Określ dziedzinę funkcji ( ) f (x) = log (−x ) + log − W-(x) 3 3 x .

Rozwiązanie

  • Szukamy pierwiastków wymiernych wielomianu. Sprawdzamy -1,1 i nic. Teraz czas na ułamki. W rachubę wchodzą
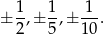
    1- 1- 1-- ± 2,± 5,± 10.

    Zaczynamy sprawdzać i znajdujemy pierwiastek 1 x = − 2 :

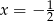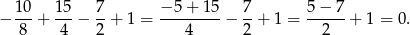
    − 10-+ 15-− 7+ 1 = −-5-+-15-− 7-+ 1 = 5−-7-+ 1 = 0. 8 4 2 4 2 2

    Powinniśmy teraz dzielić przez 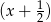(x+ 1) 2 , ale żeby nie mieć ułamków, wygodniej jest dzielić przez 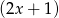(2x + 1) . My, jak zwykle, zrobimy to grupując wyrazy.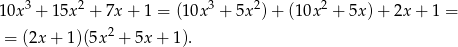

    10x 3 + 1 5x2 + 7x + 1 = (10x 3 + 5x2)+ (10x2 + 5x) + 2x + 1 = 2 = (2x + 1 )(5x + 5x + 1).

    Teraz rozkładamy trójmian w nawiasie.

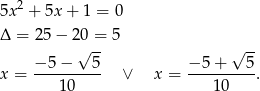
    2 5x + 5x + 1 = 0 Δ = 25− 20 = 5 √ -- √ -- x = −-5-−---5- ∨ x = −-5-+---5-. 10 10

    Mamy zatem

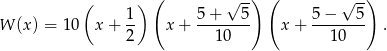
    ( ) ( √ -) ( √ -) W (x ) = 10 x + 1- x + 5-+---5- x+ 5−----5- . 2 10 10

     
    Odpowiedź: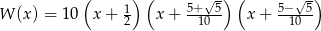 ( ) ( √- )( √ -) W (x ) = 10 x+ 1 x + 5+--5- x+ 5−--5 2 10 10

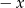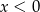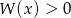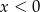  • Patrzymy najpierw na pierwszy logarytm. − x musi być dodatni, czyli musi być x < 0 . Jeżeli teraz popatrzymy na drugi, to widać, że musi być W (x) > 0 (bo x < 0 ). Z poprzedniego podpunktu wiemy, że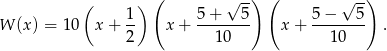
    ( ) ( ) ( 1 ) 5 + √ 5- 5− √ 5- W (x ) = 10 x + -- x + -------- x+ -------- . 2 10 10

    Ponadto

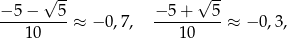
    √ -- √ -- −-5-−---5-≈ −0 ,7, −-5-+---5-≈ −0 ,3, 1 0 1 0

    więc rozwiązaniem nierówności 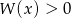W (x) > 0 jest zbiór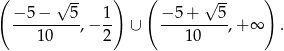

    ( ) ( ) √ -- √ -- −-5-−---5,− 1- ∪ −-5-+---5-,+ ∞ . 1 0 2 10

    Uwzględniając warunek 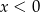x < 0 daje nam to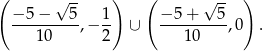

    ( √ -- ) ( √ -- ) − 5 − 5 1 − 5+ 5 ----10----,− 2- ∪ ---10----,0 .

 
Odpowiedź: (− 5− √5 1) (− 5+√ 5 ) --10---,− 2 ∪ --10---,0

Wersja PDF