Zadanie nr 9920509
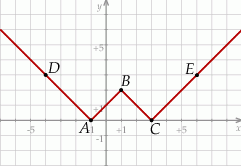
Na rysunku przedstawiono fragment wykresu funkcji 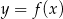 , który jest złożony z dwóch półprostych
, który jest złożony z dwóch półprostych 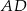 i
i 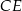 oraz dwóch odcinków
oraz dwóch odcinków 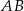 i
i 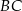 , gdzie
, gdzie 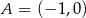 ,
, 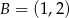 ,
, 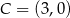 ,
, 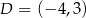 ,
, 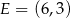 .
.
Wzór funkcji 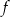 to
to
A) 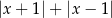 B)
B) 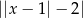 C)
C) 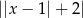 D)
D) 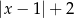
Rozwiązanie
Sposób I
Z podanego wykresu widać, że 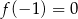 . Wśród podanych wzorów tylko wzór
. Wśród podanych wzorów tylko wzór
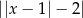
ma tę własność. Równie dobrze mogliśmy też użyć warunku: 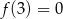 .
.
Sposób II
Jeżeli wiemy jak wygląda wykres funkcji 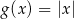 , to łatwo się domyślić jak otrzymać z tego wykresu wykres podanej funkcji
, to łatwo się domyślić jak otrzymać z tego wykresu wykres podanej funkcji 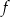 – trzeba go przesunąć o wektor
– trzeba go przesunąć o wektor ![[1,− 2]](https://img.zadania.info/zad/9920509/HzadR5x.gif) (czyli o jedną jednostkę w prawo i dwie w dół), a następnie złożyć otrzymany wzór z wartością bezwzględną (czyli odbić część pod osią
(czyli o jedną jednostkę w prawo i dwie w dół), a następnie złożyć otrzymany wzór z wartością bezwzględną (czyli odbić część pod osią 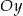 do góry).
do góry).
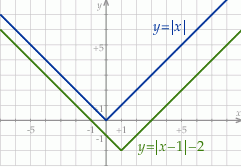
Jest to więc funkcja
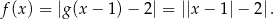
Odpowiedź: B

