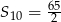/Szkoła średnia

Zadanie nr 9921906

Dodaj do ulubionych
Dodaj do rozwiązanych

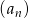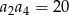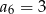W malejącym ciągu arytmetycznym (an) spełnione są warunki a2a4 = 20 oraz a6 = 3 . Wyznacz sumę 10 początkowych wyrazów tego ciągu.

Rozwiązanie

Ze wzoru 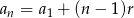an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy układ równań

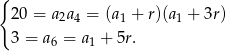
{ 20 = a2a4 = (a1 + r)(a1 + 3r ) 3 = a = a + 5r. 6 1

Z drugiego równania mamy 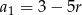a1 = 3 − 5r . Podstawiamy to wyrażenie do pierwszego równania i mamy

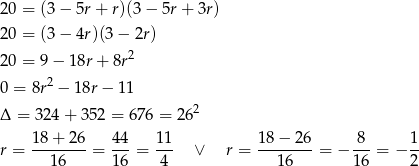
20 = (3− 5r+ r)(3 − 5r + 3r) 20 = (3− 4r)(3− 2r) 2 20 = 9− 18r+ 8r 0 = 8r2 − 1 8r− 1 1 Δ = 324 + 35 2 = 676 = 262 18+ 26 44 11 18− 26 8 1 r = --------= ---= --- ∨ r = --------= − --- = − -- 16 16 4 16 1 6 2

Ponieważ ciąg ma być malejący, mamy 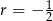1 r = − 2 . W takim razie

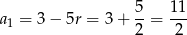
5 1 1 a1 = 3 − 5r = 3 + --= --- 2 2

oraz

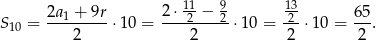
11 9 13 S 10 = 2a1 +-9r-⋅10 = 2-⋅-2-−-2-⋅10 = -2-⋅10 = 65. 2 2 2 2

 
Odpowiedź: S10 = 625

Wersja PDF