/Szkoła średnia

Zadanie nr 9923661

Dodaj do ulubionych
Dodaj do rozwiązanych

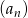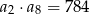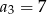W ciągu geometrycznym (an) o wyrazach dodatnich spełnione są warunki: a2 ⋅a8 = 784 oraz a3 = 7 . Iloraz tego ciąg jest równy
A) 4 B) 2 C) 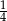14 D) 1 2

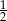
Rozwiązanie

Korzystając ze wzoru 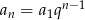n− 1 an = a1q na n -ty wyraz ciągu geometrycznego mamy

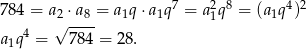
7 2 8 4 2 784 = a2 ⋅a8 = a1q⋅a1q = a1q = (a1q ) a q4 = √ 78-4 = 28. 1

Wybraliśmy dodatni pierwiastek, bo wiemy, że ciąg ma wyrazy dodatnie, a 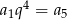a1q4 = a5 . Wiemy ponadto, że

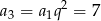
2 a3 = a1q = 7

Dzieląc dwie powyższe równości stronami mamy

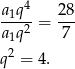
4 a1q--= 28- a1q2 7 2 q = 4.

Zatem 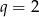q = 2 (bo ciąg jest dodatni).  
Odpowiedź: B

Wersja PDF