Zadanie nr 9928884
Dany jest trójkąt równoboczny 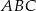 . Okrąg o średnicy
. Okrąg o średnicy 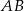 przecina bok
przecina bok 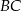 w punkcie
w punkcie 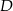 .
.
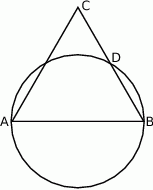
Wykaż, że 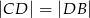 .
.
Rozwiązanie
Sposób I
Dorysujmy odcinek 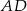 .
.
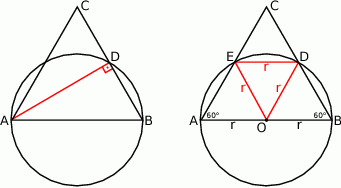
Ponieważ kąt 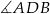 jest oparty na średnicy, więc jest prosty. To oznacza, że odcinek
jest oparty na średnicy, więc jest prosty. To oznacza, że odcinek 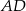 jest wysokością trójkąta
jest wysokością trójkąta 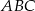 . Ale wysokość w trójkącie równobocznym pokrywa się ze środkową, czyli
. Ale wysokość w trójkącie równobocznym pokrywa się ze środkową, czyli 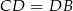 .
.
Sposób II
Niech 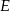 będzie punktem wspólnym okręgu i boku
będzie punktem wspólnym okręgu i boku 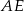 , a
, a 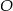 niech będzie środkiem okręgu. Połączmy punkt
niech będzie środkiem okręgu. Połączmy punkt 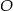 z punktami
z punktami 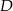 i
i 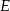 , oraz dorysujmy odcinek
, oraz dorysujmy odcinek 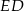 . Zauważmy, że oba trójkąty
. Zauważmy, że oba trójkąty 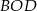 i
i 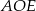 są równoramienne i każdy z nich ma kąt o mierze
są równoramienne i każdy z nich ma kąt o mierze 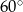 . Są zatem równoboczne. To oznacza, że
. Są zatem równoboczne. To oznacza, że
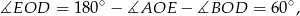
czyli trójkąt równoramienny 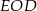 też jest równoboczny. To z kolei oznacza, że dwa kąty trójkąta
też jest równoboczny. To z kolei oznacza, że dwa kąty trójkąta 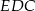 są równe
są równe 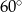 , czyli to też jest trójkąt równoboczny. Dodatkowo wszystkie narysowane trójkąty równoboczne są przystające, czyli w szczególności
, czyli to też jest trójkąt równoboczny. Dodatkowo wszystkie narysowane trójkąty równoboczne są przystające, czyli w szczególności 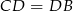 .
.
Sposób III
Dorysujmy odcinek 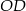 .
.
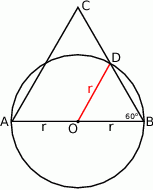
Trójkąt 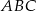 jest równoboczny i bok
jest równoboczny i bok 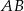 jest średnicą okręgu, zatem każdy z jego boków ma długość
jest średnicą okręgu, zatem każdy z jego boków ma długość 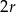 , gdzie
, gdzie  jest promieniem danego okręgu. W szczególności
jest promieniem danego okręgu. W szczególności 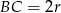 . Teraz patrzymy na trójkąt
. Teraz patrzymy na trójkąt 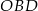 – jest on równoramienny, bo
– jest on równoramienny, bo 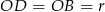 oraz jeden z jego kątów miarę
oraz jeden z jego kątów miarę 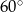 . Trójkąt ten jest więc równoboczny, czyli
. Trójkąt ten jest więc równoboczny, czyli 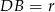 . To oznacza, że
. To oznacza, że