/Szkoła średnia

Zadanie nr 9937560

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest zbiór wszystkich graniastosłupów prawidłowych sześciokątnych, których suma długości wszystkich krawędzi jest równa 216. Oblicz długość krawędzi podstawy i wysokość tego z danych graniastosłupów, który ma największe pole powierzchni bocznej.

Rozwiązanie

Zacznijmy od rysunku.

PIC

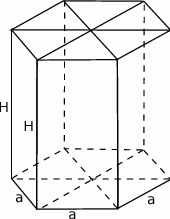
Jeżeli oznaczymy krawędź podstawy przez a , a wysokość graniastosłupa przez 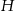H , to suma wszystkich krawędzi jest równa

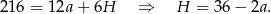
2 16 = 12a + 6H ⇒ H = 36− 2a.

Pole powierzchni bocznej jest więc równe

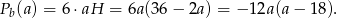
Pb(a) = 6 ⋅aH = 6a (36− 2a) = − 12a(a − 18 ).

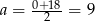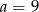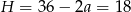Wykresem tej funkcji jest parabola o ramionach skierowanych w dół i wierzchołku w punkcie a = 0+-18-= 9 2 . Zatem największe pole boczne otrzymamy dla a = 9 i H = 36 − 2a = 1 8 .  
Odpowiedź: Krawędź podstawy: 9, wysokość: 18

Wersja PDF