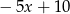/Szkoła średnia

Zadanie nr 9943548

Dodaj do ulubionych
Dodaj do rozwiązanych

Liczba 2 jest miejscem zerowym wielomianu 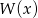W (x) . Wyznacz resztę z dzielenia tego wielomianu przez wielomian 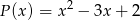P (x) = x 2 − 3x + 2 jeśli wiadomo, że w wyniku dzielenia wielomianu 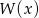W (x ) przez dwumian 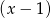(x − 1) otrzymujemy resztę 5.

Rozwiązanie

Oznaczmy szukaną resztę przez 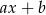ax + b (reszta ma zawsze stopień mniejszy od stopnia wielomianu, przez który dzielimy), tzn.

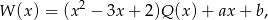
W (x) = (x 2 − 3x + 2 )Q(x )+ ax + b,

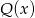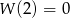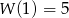dla pewnego wielomianu Q (x) . Z podanych w zadaniu informacji wynika, że W (2) = 0 oraz W (1) = 5 . Mamy zatem układ równań

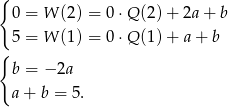
{ 0 = W (2) = 0 ⋅Q (2)+ 2a + b 5 = W (1) = 0 ⋅Q (1)+ a + b { b = − 2a a + b = 5.

Bez trudu rozwiązujemy ten układ równań, 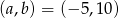(a,b) = (− 5,10) .  
Odpowiedź: − 5x + 10

Wersja PDF