/Szkoła średnia

Zadanie nr 9945461

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie całkowite wartości 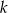k , dla których funkcja 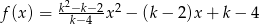2 f (x) = k-−k−k−42-x2 − (k− 2 )x+ k− 4 osiąga minimum i ma dwa różne miejsca zerowe.

Rozwiązanie

Ponieważ funkcja liniowa nie może mieć dwóch miejsc zerowych, nie musimy sprawdzać co się dzieje, gdy 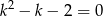k2 − k − 2 = 0 – otrzymane wtedy funkcje na pewno nie spełniają podanego warunku. Oczywiście musimy też pamiętać, że 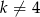k ⁄= 4 (ze względu na mianownik).

Aby parabola osiągała minimum, jej ramiona muszą być skierowane do góry, zatem

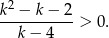
2 k-−-k-−-2-> 0. k − 4

Aby rozwiązać tę nierówność musimy rozłożyć licznik, łatwo sprawdzić, że jego pierwiastkami są liczby -1 i 2. Zatem

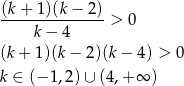
(k+-1-)(k−-2-)> 0 k − 4 (k + 1)(k − 2)(k − 4) > 0 k ∈ (− 1,2) ∪ (4,+ ∞ )

(nierówność rozwiązaliśmy patrząc na znaki wyrażeń w nawiasach – dla 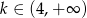k ∈ (4,+ ∞ ) wszystkie nawiasy są dodatnie, a dla 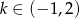k ∈ (− 1,2) dokładnie dwa są ujemne).

Parabola ma mieć dwa miejsca zerowe, czyli 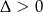Δ > 0 .

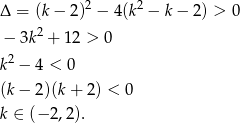
2 2 Δ = (k − 2) − 4(k − k − 2) > 0 − 3k 2 + 12 > 0 2 k − 4 < 0 (k− 2 )(k+ 2 ) < 0 k ∈ (−2 ,2).

Uwzględniając wcześniej otrzymane warunki, mamy

k ∈ (− 1,2).

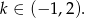
Na koniec, wypada sobie przypomnieć, że pytanie było o wartości całkowite 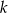k . Zatem 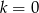k = 0 lub k = 1 .  
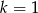Odpowiedź: 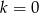k = 0 lub k = 1

Wersja PDF