Zadanie nr 9947210
Liczby naturalne 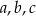 są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba
są większe od 1 oraz są kolejnymi wyrazami ciągu geometrycznego. Liczba  spełnia warunek
spełnia warunek
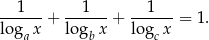
Wykaż, że  jest sześcianem liczby naturalnej.
jest sześcianem liczby naturalnej.
Rozwiązanie
Będziemy oczywiście korzystać ze wzoru
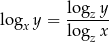
na zmianę podstawy logarytmu. Na razie nie przejmujmy się założeniem o ciągu geometrycznym i spróbujmy uprościć daną równość (zmieniamy podstawy wszystkich logarytmów na  ).
).
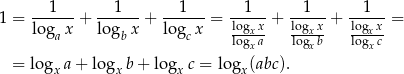
To oznacza, że 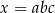 . Nadszedł czas, by skorzystać z tego, że ciąg
. Nadszedł czas, by skorzystać z tego, że ciąg 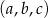 jest ciągiem geometrycznym. W szczególności
jest ciągiem geometrycznym. W szczególności 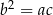 i mamy
i mamy
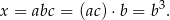
Zatem rzeczywiście  jest sześcianem liczby naturalnej
jest sześcianem liczby naturalnej 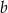 .
.

