/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 12 marca 2016 Czas pracy: 180 minut
Zadania zamknięte
Dana jest funkcja 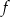 określona wzorem
określona wzorem 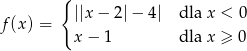
Równanie 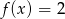 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.
Rysunek przedstawia wykres funkcji 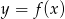 .
.
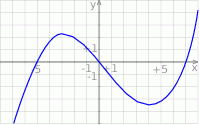
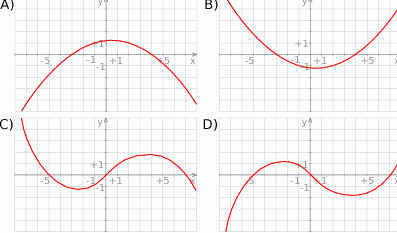
Wskaż wykres funkcji 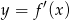 .
.
Ciąg 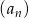 jest określony wzorem
jest określony wzorem 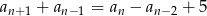 dla każdej liczby naturalnej
dla każdej liczby naturalnej 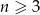 . Wiadomo ponadto, że
. Wiadomo ponadto, że 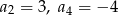 i
i 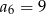 . Wyraz
. Wyraz 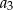 jest równy
jest równy
A) 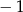 B) 0 C) 5 D)
B) 0 C) 5 D) 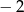
Zbiór 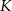 – to zbiór wszystkich liczb rzeczywistych
– to zbiór wszystkich liczb rzeczywistych  , dla których wartość liczbowa wyrażenia
, dla których wartość liczbowa wyrażenia 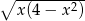 jest liczbą rzeczywistą. Zatem
jest liczbą rzeczywistą. Zatem
A) 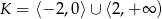
B) 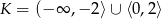
C) 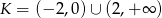
D) 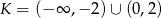
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano damę jeżeli wiadomo, że wylosowana karta nie jest ani kierem ani królem?
A) 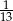 B)
B) 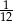 C)
C) 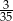 D)
D) 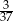
Zadania otwarte
Wyznacz największą liczbę całkowitą spełniającą nierówność 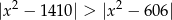 .
.
Oblicz granicę
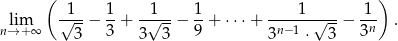
Na ile sposobów można umieścić 6 ponumerowanych kul w czterech szufladach tak, aby w jednej z szuflad były dokładnie 4 kule?
Udowodnij, że dla każdych dwóch liczb rzeczywistych 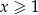 i
i 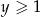 prawdziwa jest nierówność
prawdziwa jest nierówność
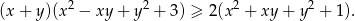
Długości boków równoległoboku są równe 13 i 21, a jego pole wynosi 252. Oblicz długości przekątnych tego równoległoboku.
Przez każde dwa sąsiednie wierzchołki czworokąta 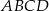 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
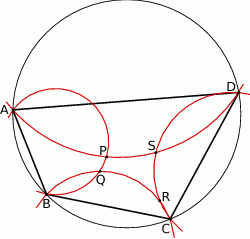
Wykaż, że punkty 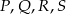 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Rozwiąż równanie 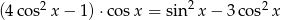 , dla
, dla 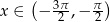 .
.
Dany jest okrąg 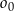 o równaniu
o równaniu 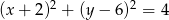 . W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W drugiej „ćwiartce” układu współrzędnych istnieją dwa okręgi 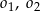 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 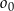 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 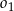 oraz
oraz 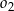 .
.
Dany jest trójmian kwadratowy 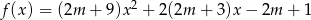 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 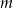 , dla których trójmian
, dla których trójmian 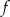 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 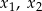 , spełniające warunek
, spełniające warunek 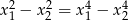 .
.
Podstawą ostrosłupa 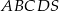 jest prostokąt
jest prostokąt 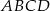 . Spodkiem wysokości ostrosłupa jest środek
. Spodkiem wysokości ostrosłupa jest środek 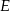 krawędzi
krawędzi 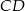 . Oblicz tangens kąta między ścianami bocznymi
. Oblicz tangens kąta między ścianami bocznymi 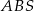 i
i 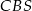 tego ostrosłupa jeżeli
tego ostrosłupa jeżeli 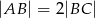 i
i 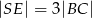 .
.
Na półkuli o promieniu 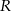 opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?
opisano stożek w ten sposób, że środek podstawy stożka pokrywa się ze środkiem kuli. Jaka jest najmniejsza możliwa objętość tego stożka?

