/Szkoła średnia
Egzamin Maturalny
z Matematyki poziom rozszerzony 11 maja 2021 Czas pracy: 180 minut
Zadania zamknięte
Różnica 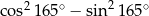 jest równa
jest równa
A) 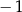 B)
B) 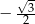 C)
C) 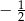 D)
D) 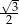
Na rysunku przedstawiono fragment wykresu funkcji 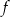 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
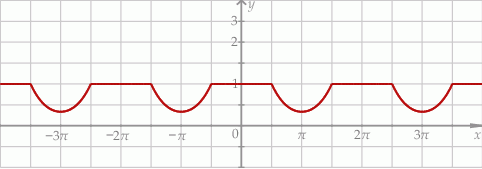
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 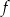 .
.
A) 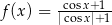 B)
B) 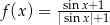 C)
C) 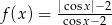 D)
D) 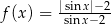
Wielomian 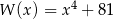 jest podzielny przez
jest podzielny przez
A) 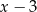 B)
B) 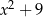 C)
C) 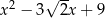 D)
D) 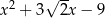
Liczba różnych pierwiastków równania 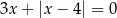 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Zadania otwarte
Oblicz granicę 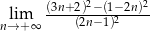 .
.
Niech 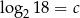 . Wykaż, że
. Wykaż, że 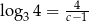 .
.
Rozwiąż nierówność
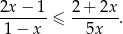
Dany jest trójkąt równoboczny 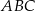 . Na bokach
. Na bokach 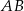 i
i 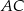 wybrano punkty – odpowiednio –
wybrano punkty – odpowiednio – 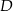 i
i 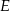 takie, że
takie, że 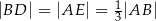 . Odcinki
. Odcinki 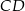 i
i 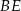 przecinają się w punkcie
przecinają się w punkcie 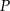 (zobacz rysunek).
(zobacz rysunek).
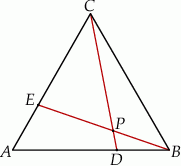
Wykaż, że pole trójkąta 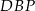 jest 21 razy mniejsze od pola trójkąta
jest 21 razy mniejsze od pola trójkąta 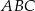 .
.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 15, jeśli wiadomo, że jest ona podzielna przez 18.
Prosta przechodząca przez punkty 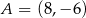 i
i 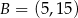 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 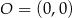 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 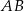 .
.
Wyznacz wszystkie wartości parametru 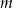 , dla których trójmian kwadratowy
, dla których trójmian kwadratowy
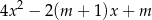
ma dwa różne pierwiastki rzeczywiste 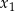 oraz
oraz 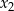 , spełniające warunki:
, spełniające warunki:
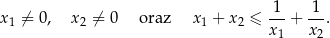
Rozwiąż równanie 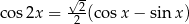 w przedziale
w przedziale 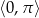 .
.
Dany jest trójkąt prostokątny 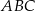 . Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta
. Promień okręgu wpisanego w ten trójkąt jest pięć razy krótszy od przeciwprostokątnej tego trójkąta. Oblicz sinus tego z kątów ostrych trójkąta 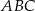 , który ma większą miarę.
, który ma większą miarę.
Dane są parabola o równaniu 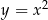 oraz punkty
oraz punkty 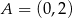 i
i 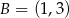 (zobacz rysunek).
(zobacz rysunek).
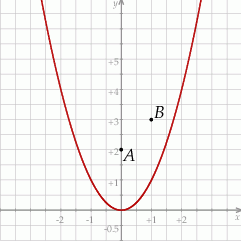
Rozpatrujemy wszystkie trójkąty 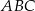 , których wierzchołek
, których wierzchołek 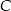 leży na tej paraboli. Niech
leży na tej paraboli. Niech 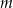 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 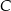 .
.
- Wyznacz pole
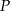 trójkąta
trójkąta 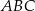 jako funkcję zmiennej
jako funkcję zmiennej 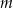 .
. - Wyznacz wszystkie wartości
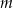 , dla których trójkąt
, dla których trójkąt 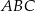 jest ostrokątny.
jest ostrokątny.
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 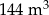 . Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 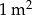 dna
dna
– 75 zł za 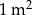 ściany bocznej.
ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.

