Zadanie nr 9953664
Na trójkącie 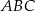 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 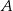 (zobacz rysunek obok).
(zobacz rysunek obok).
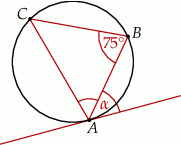
Jeżeli 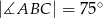 i kąt dopisany
i kąt dopisany  jest równy
jest równy 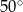 , to kąt
, to kąt 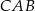 ma miarę:
ma miarę:
A) 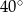 B)
B) 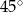 C)
C) 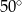 D)
D) 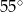
Rozwiązanie
Sposób I
Na mocy twierdzenia o stycznej i siecznej 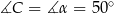 . W takim razie
. W takim razie
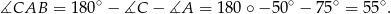
Sposób II
Dorysujmy promienie 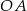 i
i 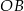 .
.
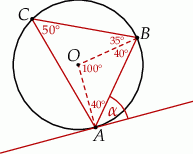
Trójkąt 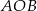 jest równoramienny, więc
jest równoramienny, więc
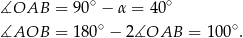
W takim razie (twierdzenie o kątach: wpisanym i środkowym)
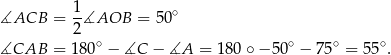
Odpowiedź: D

