Zadanie nr 9955043
Wiadomo, że 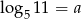 . Wykaż, że
. Wykaż, że 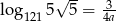 .
.
Rozwiązanie
Sposób I
Skorzystamy z następującego wzoru
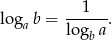
Liczymy
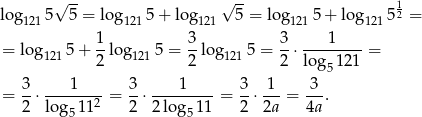
Sposób II
Korzystamy ze wzoru na zmianę podstawy logarytmu.
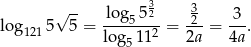
Sposób III
Korzystamy ze wzoru na zmianę podstawy logarytmu.
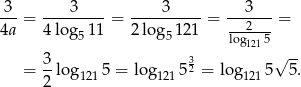
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wiadomo, że 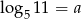 . Wykaż, że
. Wykaż, że 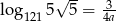 .
.
Sposób I
Skorzystamy z następującego wzoru
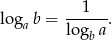
Liczymy
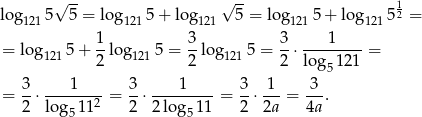
Sposób II
Korzystamy ze wzoru na zmianę podstawy logarytmu.
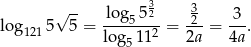
Sposób III
Korzystamy ze wzoru na zmianę podstawy logarytmu.