/Szkoła średnia

Zadanie nr 9956355

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 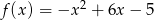2 f(x ) = −x + 6x − 5 .

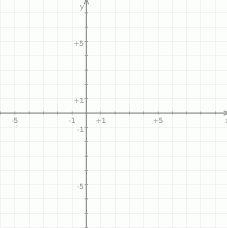
  • Narysuj parabolę, która jest wykresem funkcji 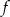f i zaznacz na rysunku współrzędne jej wierzchołka oraz punktów przecięcia paraboli z osiami układu współrzędnych.
  • Odczytaj z wykresu zbiór wartości funkcji f .
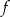  • Rozwiąż nierówność f(x) ≥ 0 .
PIC

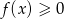Rozwiązanie

  • Ponieważ współczynnik przy 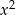2 x jest ujemny, ramiona paraboli są skierowane w dół, sprawdźmy gdzie jest jej wierzchołek i miejsca zerowe.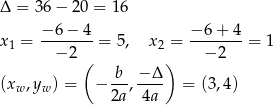
    Δ = 36− 20 = 16 x1 = −-6-−-4 = 5, x2 = −-6+--4 = 1 − 2 ( ) − 2 b − Δ (xw,yw ) = − --, ---- = (3,4) 2a 4a

    Teraz bez trudu szkicujemy żądany wykres.

    PIC
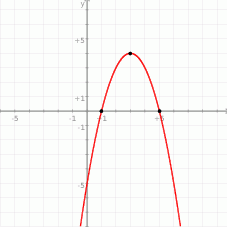
  • Odczytujemy z wykresu wszystkie możliwe wartości 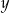y punktów na wykresie.  
    Odpowiedź: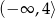 (− ∞ ,4⟩
  • Odczytujemy z wykresu lub rozwiązujemy algebraicznie
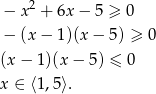
    2 − x + 6x − 5 ≥ 0 − (x− 1)(x − 5) ≥ 0 (x − 1)(x − 5) ≤ 0 x ∈ ⟨1,5⟩.

     
    Odpowiedź: x ∈ ⟨1,5⟩

Wersja PDF