Zadanie nr 9956525
Rozwiąż nierówność 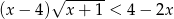 .
.
Rozwiązanie
Sposób I
Zróbmy podstawienie 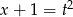 . Wtedy
. Wtedy 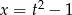 i podana nierówność przyjmuje postać.
i podana nierówność przyjmuje postać.
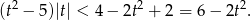
Mamy dwa przypadki. Jeżeli 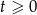 , to
, to
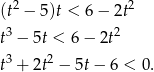
Łatwo sprawdzić, że pierwiastkiem tego wielomianu jest 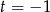 . Dzielimy zatem przez dwumian
. Dzielimy zatem przez dwumian 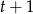 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
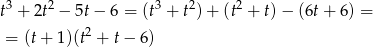
Dalej, 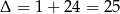 ,
, 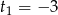 ,
, 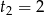 . Rozwiązaniem tej nierówności jest więc zbiór
. Rozwiązaniem tej nierówności jest więc zbiór
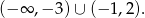
Ponieważ miało być 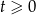 , mamy
, mamy 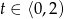 . Ponieważ
. Ponieważ 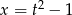 mamy stąd
mamy stąd 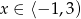 .
.
Podobnie w przypadku, gdy 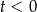 ,
,
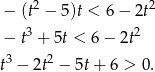
Tu pierwiastkiem jest 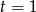 oraz
oraz
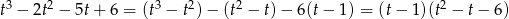
Dalej, 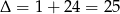 ,
, 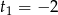 ,
, 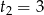 . Stąd
. Stąd 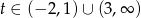 . Ponieważ
. Ponieważ 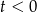 , więc
, więc 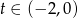 . Stąd
. Stąd 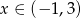 .
.
Sposób II
Tym razem spróbujemy nierówność sprowadzić do zwykłej nierówności wielomianowej bez podstawiania. Zauważmy na początku, że wyrażenie pod pierwiastkiem musi być nieujemne, czyli 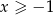 . Ponadto jeżeli
. Ponadto jeżeli 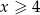 to lewa strona jest nieujemna a prawa ujemna, czyli nierówność nie ma rozwiązań.
to lewa strona jest nieujemna a prawa ujemna, czyli nierówność nie ma rozwiązań.
Możemy więc założyć, że 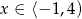 . Przy takim założeniu lewa strona jest niedodatnia.
. Przy takim założeniu lewa strona jest niedodatnia.
Jaki jest znak prawej strony? Jeżeli 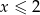 to prawa strona jest nieujmena i nierówność będzie spełniona.
to prawa strona jest nieujmena i nierówność będzie spełniona.
Pozostał nam przypadek 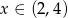 . W tej sytuacji obie strony są ujemne, więc mnożąc obie strony przez -1 otrzymamy nierówność z dodatnimi stronami
. W tej sytuacji obie strony są ujemne, więc mnożąc obie strony przez -1 otrzymamy nierówność z dodatnimi stronami
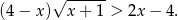
Podnosimy nierówność stronami do kwadratu.
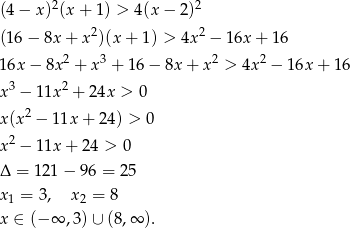
Uwzględniając wszystkie rozpatrzone przypadki mamy 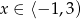 .
.
Odpowiedź: