Zadanie nr 9958237
Punkt 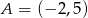 leży na prostej
leży na prostej 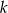 prostopadłej do prostej o równaniu
prostopadłej do prostej o równaniu 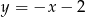 . Prosta
. Prosta 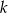 ma równanie
ma równanie
A) 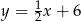 B)
B) 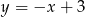 C)
C) 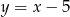 D)
D) 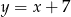
Rozwiązanie
Proste 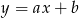 oraz
oraz 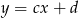 są prostopadłe jeżeli
są prostopadłe jeżeli 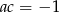 . Zatem szukana prosta musi mieć współczynnik kierunkowy (liczbę przy
. Zatem szukana prosta musi mieć współczynnik kierunkowy (liczbę przy  ) równy 1. Jest to więc prosta
) równy 1. Jest to więc prosta 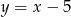 lub
lub 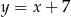 . Wiemy ponadto, że po podstawieniu
. Wiemy ponadto, że po podstawieniu 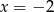 mamy otrzymać
mamy otrzymać 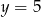 , to oznacza, że poprawne jest równanie:
, to oznacza, że poprawne jest równanie: 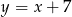 .
.
Odpowiedź: D

