Zadanie nr 9962731
Ze zbioru liczb 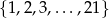 losujemy jednocześnie siedem liczb i ustawiamy je w kolejności rosnącej
losujemy jednocześnie siedem liczb i ustawiamy je w kolejności rosnącej 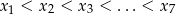 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 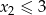 .
.
Rozwiązanie
Wszystkich możliwych wyborów 7 liczb z 21 jest
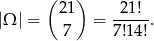
Policzmy zdarzenia sprzyjające. Jeżeli 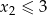 , to
, to 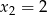 lub
lub 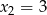 (nie może być
(nie może być 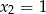 , bo
, bo 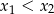 ). W pierwszej sytuacji mamy
). W pierwszej sytuacji mamy 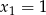 , a w drugiej
, a w drugiej 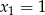 lub
lub 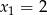 . Policzmy ile jest takich konfiguracji.
. Policzmy ile jest takich konfiguracji.
W pierwszej sytuacji, gdy 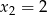 i
i 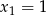 sprawa jest prosta,
sprawa jest prosta, 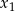 i
i 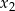 mamy wybrane, a pozostałe 5 liczb wybieramy spośród 19. Jest więc
mamy wybrane, a pozostałe 5 liczb wybieramy spośród 19. Jest więc
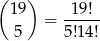
takich konfiguracji.
W drugiej sytuacji, gdy 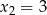 i
i 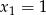 lub
lub 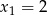 jest podobnie,
jest podobnie, 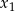 i
i 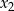 mamy wybrane (ale teraz są dwie możliwości), a pozostałe 5 liczb wybieramy spośród 18. Jest więc
mamy wybrane (ale teraz są dwie możliwości), a pozostałe 5 liczb wybieramy spośród 18. Jest więc
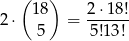
takich sytuacji.
Mamy więc
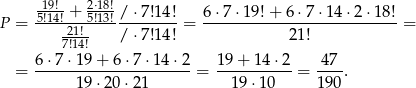
Odpowiedź: