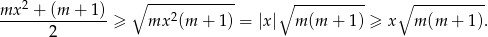/Szkoła średnia

Zadanie nr 9963925

Dodaj do ulubionych
Dodaj do rozwiązanych

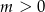Udowodnij, że dowolne liczby rzeczywiste x i m > 0 spełniają nierówność

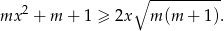
∘ ---------- mx 2 + m + 1 ≥ 2x m (m + 1).

Rozwiązanie

Sposób I

Jeżeli zapiszemy daną nierówność w postaci

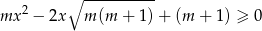
∘ ---------- mx 2 − 2x m(m + 1) + (m + 1) ≥ 0

to widać, że mamy do czynienia ze zwykłą nierównością kwadratową. Liczymy 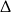Δ -ę.

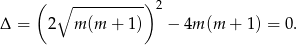
( ∘ ---------) 2 Δ = 2 m(m + 1) − 4m (m + 1) = 0.

Ponieważ z założenia 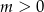m > 0 wykres trójmianu znajdującego się po lewej stronie nierówności jest parabolą o ramionach skierowanych w górę, która jest styczna do osi 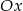Ox . To oznacza, że funkcja ta nie przyjmuje wartości ujemnych.

Sposób II

Przekształcamy daną nierówność w sposób równoważny.

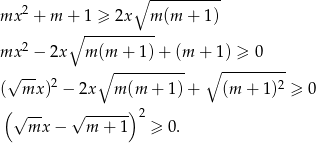
2 ∘ ---------- mx + m + 1 ≥ 2x m (m + 1) ∘ ---------- mx 2 − 2x m (m + 1 )+ (m + 1) ≥ 0 √ -- ∘ ---------- ∘ --------- ( mx )2 − 2x m (m + 1 )+ (m + 1)2 ≥ 0 ( ) √mx- − √m--+--1 2 ≥ 0 .

Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musi być spełniona.

Sposób III

Korzystamy z nierówności

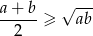
√ --- a+--b-≥ ab 2

między średnią arytmetyczną i geometryczną.

Mamy zatem

∘ ------------ ∘ ---------- ∘ ---------- mx-2 +-(m-+-1)- 2 2 ≥ mx (m + 1) = |x| m (m + 1 ) ≥ x m (m + 1).
Wersja PDF