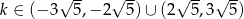/Szkoła średnia

Zadanie nr 9964695

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 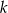k , dla których równanie 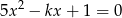5x 2 − kx + 1 = 0 ma dwa różne pierwiastki, których różnica jest liczbą z przedziału (0,1) .

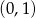Rozwiązanie

Sprawdźmy najpierw kiedy równanie ma dwa pierwiastki

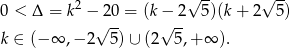
2 √ -- √ -- 0 < Δ = k −√20-= (k −√ 2- 5)(k+ 2 5) k ∈ (− ∞ ,− 2 5) ∪ (2 5,+ ∞ ).

Sposób I

Zauważmy, że jeżeli różnica pierwiastków ma być dodatnia to musimy od większego pierwiastka odejmować mniejszy. Korzystając ze wzorów na pierwiastki mamy więc nierówność.

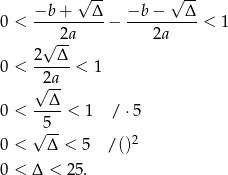
−b + √ Δ- −b − √ Δ- 0 < ----------− ----------< 1 √ 2a 2a 2 Δ 0 < ----- < 1 √2a- 0 < --Δ-< 1 / ⋅5 5 √ -- 2 0 < Δ < 5 /() 0 < Δ < 2 5.

Lewą nierówność już rozwiązywaliśmy, więc zajmijmy się prawą nierównością

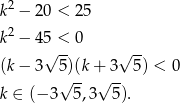
2 k − 2 0 < 25 k2 − 4 5 < 0 √ -- √ -- (k− 3 5)(k+ 3 5) < 0 k ∈ (− 3√ 5,3√ 5).

W połączeniu z nierównością 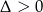Δ > 0 daje to rozwiązanie:

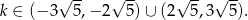
√ -- √ -- √ -- √ -- k ∈ (− 3 5,− 2 5) ∪ (2 5,3 5).

Sposób II

Tym razem skorzystamy ze wzorów Viète’a. Jeżeli oznaczymy przez 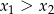x1 > x2 pierwiastki trójmianu, to nierówność 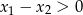x 1 − x 2 > 0 jest spełniona automatycznie. Pozostało zająć się nierównością

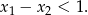
x1 − x2 < 1.

Obie strony są dodatnie, więc podnosimy nierówność stronami do kwadratu (żeby móc skorzystać ze wzorów Viète’a).

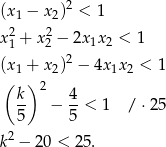
2 (x1 − x2) < 1 x21 + x22 − 2x1x2 < 1 2 (x1 + x2) − 4x 1x2 < 1 ( k) 2 4 -- − --< 1 / ⋅25 5 5 k2 − 2 0 < 25.

Tę nierówność rozwiązujemy dokładnie tak samo jak w pierwszym sposobie.  
Odpowiedź: √ -- √ -- √ -- √ -- k ∈ (− 3 5,− 2 5) ∪ (2 5,3 5 )

Wersja PDF