Zadanie nr 9966256
W grupie 24 osób (mężczyzn i kobiet) jest 3 razy więcej kobiet niż mężczyzn. Z grupy tej losujemy 2 osoby. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowano osoby różnej płci to
A) 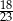 B)
B)  C)
C) 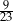 D)
D) 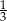
Rozwiązanie
Jeżeli mężczyzn jest  , to kobiet jest
, to kobiet jest 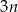 i
i
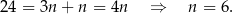
Sposób I
Parę osób 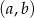 możemy wylosować na
możemy wylosować na
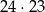
sposoby. Wśród tych par jest
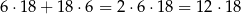
par z osobami różnych płci. Interesujące nas prawdopodobieństwo jest więc równe
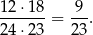
Sposób II
Dwie osoby 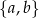 możemy wylosować na
możemy wylosować na
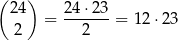
sposoby. Wśród tych par jest
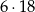
(nieuporządkowanych) par z osobami różnej płci. Interesujące nas prawdopodobieństwo jest więc równe
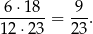
Odpowiedź: C

