Zadanie nr 9967350
Na zewnątrz kwadratu 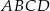 na bokach
na bokach 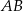 i
i 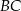 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 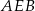 i
i 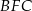 . Uzasadnij, że proste
. Uzasadnij, że proste 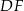 i
i 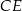 są prostopadłe.
są prostopadłe.
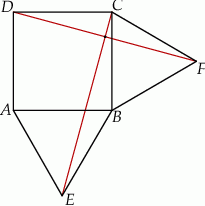
Rozwiązanie
Sposób I
Patrzymy na trójkąt 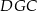 . Pokażemy, że w tym trójkącie
. Pokażemy, że w tym trójkącie 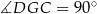 .
.
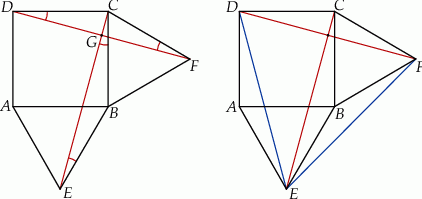
Zauważmy najpierw, że każdy z trójkątów 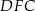 i
i 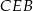 jest równoramienny oraz
jest równoramienny oraz
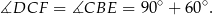
Trójkąty 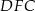 i
i 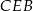 są więc przystające. W szczególności
są więc przystające. W szczególności
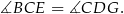
Patrzymy na trójkąt 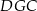 .
.
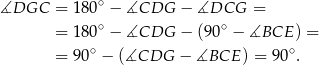
Sposób II
Tak jak poprzednio stwierdzamy, że trójkąty 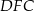 i
i 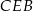 są równoramienne i kąt między ramionami ma miarę
są równoramienne i kąt między ramionami ma miarę 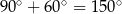 . Zatem
. Zatem
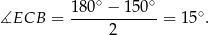
Zatem
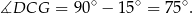
To oznacza, że prosta 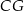 jest dwusieczną w trójkącie równoramiennym
jest dwusieczną w trójkącie równoramiennym 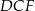 . Dwusieczna kąta między ramionami kąta w trójkącie równoramiennym pokrywa się z jego wysokością, zatem prosta
. Dwusieczna kąta między ramionami kąta w trójkącie równoramiennym pokrywa się z jego wysokością, zatem prosta 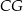 jest prostopadła do
jest prostopadła do 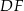 .
.
Sposób III
Dorysujmy odcinki 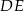 i
i 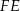 . Zauważmy, że trójkąty
. Zauważmy, że trójkąty 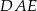 i
i 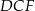 są równoramienne (
są równoramienne (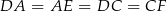 ) oraz w każdym z nich kąt między ramionami ma miarę
) oraz w każdym z nich kąt między ramionami ma miarę 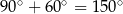 . Trójkąty te są więc przystające, czyli
. Trójkąty te są więc przystające, czyli 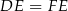 . To jednak oznacza, że czworokąt
. To jednak oznacza, że czworokąt 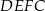 jest deltoidem. Przekątne deltoidu są prostopadłe, czyli
jest deltoidem. Przekątne deltoidu są prostopadłe, czyli 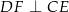 .
.
Sposób IV
Niech 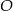 będzie obrotem o
będzie obrotem o 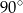 względem środka kwadratu
względem środka kwadratu 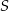 .
.
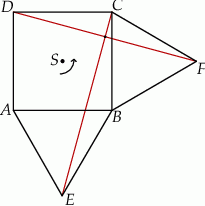
Obrót ten przekształca trójkąt 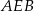 na
na 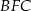 , oraz punkt
, oraz punkt 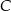 na punkt
na punkt 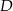 . Zatem
. Zatem 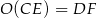 . To oznacza, że odcinki te są prostopadłe.
. To oznacza, że odcinki te są prostopadłe.

