/Szkoła średnia

Zadanie nr 9970815

Dodaj do ulubionych
Dodaj do rozwiązanych

Rosnące, trzywyrazowe ciągi arytmetyczny i geometryczny mają pierwsze wyrazy równe 9. Trzecie wyrazy tych ciągów są także równe. Drugi wyraz ciągu arytmetycznego jest o 2 większy od drugiego wyrazu ciągu geometrycznego. Wyznacz te ciągi.

Rozwiązanie

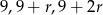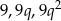Oznaczmy 3 początkowe wyrazy szukanych ciągów przez 9,9+ r,9+ 2r oraz 9,9q ,9q2 . Mamy zatem układ

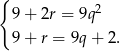
{ 9 + 2r = 9q2 9 + r = 9q + 2.

Podstawiamy 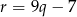r = 9q − 7 z drugiego równania do pierwszego

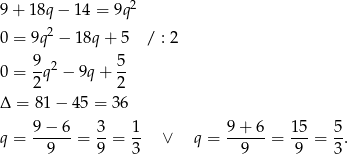
2 9 + 18q − 14 = 9q 0 = 9q 2 − 1 8q+ 5 / : 2 0 = 9q2 − 9q + 5- 2 2 Δ = 81 − 45 = 3 6 9− 6 3 1 9 + 6 15 5 q = ------= --= -- ∨ q = ------= ---= -. 9 9 3 9 9 3

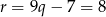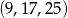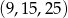Ponieważ ciągi mają być rosnące, pierwsze rozwiązanie odrzucamy i mamy r = 9q − 7 = 8 . Daje to nam ciągi (9 ,17,25) oraz (9,15,25) .  
Odpowiedź: 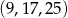(9,17 ,2 5) oraz (9 ,15,25)

Wersja PDF