Zadanie nr 9971751
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
Rozwiązanie
Sposób I
Niech 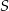 będzie punktem przecięcia przekątnych, a
będzie punktem przecięcia przekątnych, a 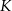 i
i 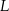 środkami podstaw
środkami podstaw 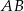 i
i 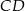 .
.
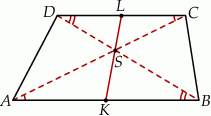
Wiemy, że trójkąty 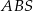 i
i 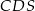 są podobne, oznaczmy skalę ich podobieństwa przez
są podobne, oznaczmy skalę ich podobieństwa przez 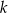 . W takim razie jednokładność
. W takim razie jednokładność 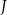 o środku w
o środku w 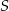 i skali
i skali 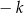 przekształca trójkąt
przekształca trójkąt 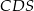 na trójkąt
na trójkąt 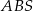 . W szczególności przekształca środek boku
. W szczególności przekształca środek boku 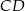 na środek boku
na środek boku 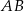 . Zatem
. Zatem 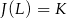 . To jednak oznacza, że środek
. To jednak oznacza, że środek 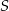 jednokładności leży na odcinku
jednokładności leży na odcinku 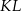 .
.
Sposób II
Niech 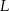 będzie środkiem podstawy
będzie środkiem podstawy 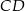 ,
, 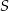 punktem przecięcia się przekątnych, a
punktem przecięcia się przekątnych, a 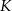 punktem wspólnym odcinków
punktem wspólnym odcinków 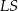 i
i 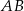 . Zauważmy, że mamy dwie pary trójkątów podobnych:
. Zauważmy, że mamy dwie pary trójkątów podobnych: 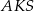 i
i 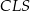 oraz
oraz 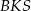 i
i 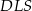 . Z tych podobieństw mamy
. Z tych podobieństw mamy
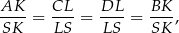
co oznacza, że 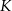 jest środkiem podstawy
jest środkiem podstawy 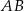 .
.
Sposób III
Teza jest oczywista dla równoległoboku, więc załóżmy, że trapez ma boki nierównoległe i niech  będzie punktem wspólnym zwierających je prostych.
będzie punktem wspólnym zwierających je prostych.
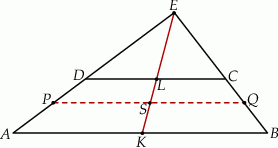
Zauważmy, że jeżeli  jest środkiem odcinka
jest środkiem odcinka 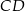 to prosta
to prosta 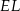 jest środkową trójkąta
jest środkową trójkąta 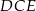 . Na mocy twierdzenia Talesa prosta ta dzieli każdy poziomy odcinek (tzn. odcinek równoległy do
. Na mocy twierdzenia Talesa prosta ta dzieli każdy poziomy odcinek (tzn. odcinek równoległy do 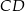 ), którego końce leżą na prostych
), którego końce leżą na prostych 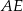 i
i 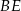 na dwie równe części. W szczególności prosta ta przechodzi przez środek
na dwie równe części. W szczególności prosta ta przechodzi przez środek 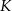 podstawy
podstawy 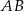 . Ponadto, jeżeli
. Ponadto, jeżeli 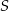 jest punktem wspólnym tej prostej z odcinkiem
jest punktem wspólnym tej prostej z odcinkiem 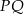 równoległym do
równoległym do 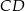 i przechodzącym przez punkt przecięcia przekątnych to
i przechodzącym przez punkt przecięcia przekątnych to 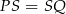 . Jednak jak wiadomo tę samą własność ma punkt przecięcia przekątnych trapezu. Zatem
. Jednak jak wiadomo tę samą własność ma punkt przecięcia przekątnych trapezu. Zatem 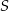 musi być punktem przecięcia przekątnych.
musi być punktem przecięcia przekątnych.

