Zadanie nr 9976769
Reszta z dzielenia wielomianu 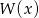 przez dwumian
przez dwumian 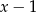 jest równa 1, zaś reszta z dzielenia tego wielomianu przez
jest równa 1, zaś reszta z dzielenia tego wielomianu przez 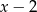 jest równa 4. Wyznacz resztę z dzielenia wielomianu
jest równa 4. Wyznacz resztę z dzielenia wielomianu 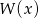 przez wielomian
przez wielomian 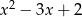 .
.
Rozwiązanie
Z podanych informacji wynika, że
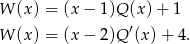
Jak podstawimy w tych równościach 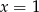 i
i 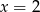 odpowiednio, to otrzymamy
odpowiednio, to otrzymamy 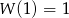 i
i 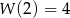 (swoją drogą warto zapamiętać, że reszta z dzielenia
(swoją drogą warto zapamiętać, że reszta z dzielenia 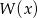 przez
przez  to po prostu
to po prostu 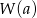 ).
).
Reszta 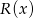 z dzielenia
z dzielenia 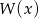 przez
przez 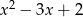 jest wielomianem stopnia 1 takim, że
jest wielomianem stopnia 1 takim, że
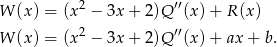
Podstawiając w tej równości 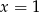 i
i 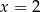 otrzymujemy
otrzymujemy
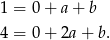
Odejmując od drugiej równości pierwszą (żeby skrócić 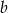 ) dostajemy
) dostajemy 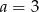 . Stąd
. Stąd 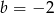 .
.
Odpowiedź: