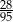/Szkoła średnia

Zadanie nr 9989598

Dodaj do ulubionych
Dodaj do rozwiązanych

W koszu znajdują się owoce: 12 jabłek i 8 pomarańczy. Wyjmujemy kolejno trzy owoce, nie odkładając ich do kosza. Jakie jest prawdopodobieństwo, że wylosujemy dokładnie dwie pomarańcze.

Rozwiązanie

Sposób I

Za zdarzenia elementarne przyjmijmy trójki 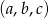(a,b,c) wyciągniętych owoców. Pierwszy owoc możemy wyjąć na 20 sposobów, drugi na 19, a trzeci na 18. Zatem

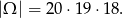
|Ω | = 20 ⋅19 ⋅18.

W zdarzeniach sprzyjających muszą być dokładnie dwie pomarańcze, więc zdarzenia sprzyjające są postaci

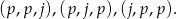
(p,p,j),(p,j,p),(j,p,p ).

W każdym z takich zdarzeń pierwszą pomarańczę możemy wybrać na 8 a drugą na 7 sposobów. Jabłko możemy wybrać na 12 sposobów. Jest więc

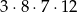
3⋅8 ⋅7 ⋅12

zdarzeń sprzyjających. Prawdopodobieństwo jest więc równe

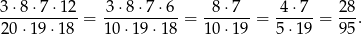
3-⋅8-⋅7⋅-12 = 3⋅-8⋅7-⋅6-= -8-⋅7--= -4⋅7--= 28. 20⋅1 9⋅1 8 10⋅1 9⋅18 10 ⋅19 5 ⋅19 95

Sposób II

Tym razem za zdarzenia sprzyjające przyjmijmy trójelementowe zbiory 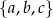{a ,b,c} wylosowanych owoców. Mamy więc

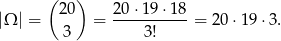
( 20) 20 ⋅19 ⋅18 |Ω | = = -----------= 20 ⋅19⋅ 3. 3 3 !

W zdarzeniach sprzyjających musimy wybrać dwie pomarańcze – możemy to zrobić na

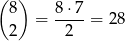
( ) 8 = 8-⋅7 = 2 8 2 2

sposobów. Do tego musimy dobrać jeszcze jedno jabłko, co możemy zrobić na 12 sposobów. Jest więc

12 ⋅28

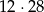
zdarzeń sprzyjających i prawdopodobieństwo wynosi

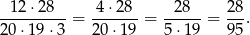
1 2⋅28 4 ⋅28 28 28 --------- = -------= ------= ---. 20 ⋅19 ⋅3 20⋅1 9 5 ⋅19 95

 
Odpowiedź: 28 95

Wersja PDF