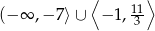/Szkoła średnia

Zadanie nr 9994084

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 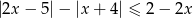|2x − 5|− |x+ 4| ≤ 2− 2x .

Rozwiązanie

Aby opuścić wartości bezwzględne rozważamy trzy przypadki.
Jeżeli 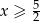x ≥ 52 to mamy nierówność

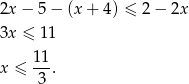
2x − 5 − (x + 4) ≤ 2− 2x 3x ≤ 11 x ≤ 11. 3

Mamy więc w tym przypadku zbiór rozwiązań 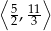⟨ 5 11⟩ 2, 3 .
Jeżeli 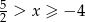5> x ≥ − 4 2 to mamy nierówność

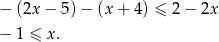
− (2x − 5)− (x+ 4) ≤ 2− 2x − 1 ≤ x.

Mamy zatem w tym przypadku zbiór rozwiązań: 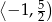⟨ 5) − 1, 2 .
Jeżeli wreszcie 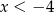x < − 4 to mamy nierówność

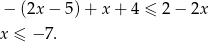
− (2x − 5)+ x+ 4 ≤ 2− 2x x ≤ − 7.

W tym przypadku zbiorem rozwiązań jest więc przedział 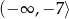(− ∞ ,− 7⟩ .
Łącząc wszystkie otrzymane zbiory rozwiązań otrzymujemy zbiór

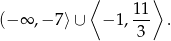
⟨ 11⟩ (− ∞ ,− 7⟩∪ − 1, --- . 3

 
Odpowiedź: ⟨ ⟩ (− ∞ ,− 7⟩ ∪ − 1, 113

Wersja PDF