/Szkoła średnia

Zadanie nr 9995462

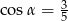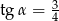Wykaż, że nie istnieje kąt α , taki, że 3 cos α = 5 i 3 tgα = 4 .

Wersja PDF

Rozwiązanie

Sposób I

Z jedynki trygonometrycznej wyznaczamy wartość sinus

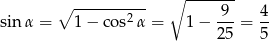
∘ ------- ∘ -------2-- -9- 4- sin α = 1− cos α = 1 − 25 = 5

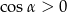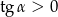(sinus musi być dodatni, bo cosα > 0 i tg α > 0 ). To jednak nie zgadza się z podanym tangensem, bo w takim razie

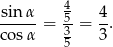
sin α 4 4 ----- = 53-= -. co sα 5 3

Zatem nie istnieje kąt α który spełniałby obie równości.

Sposób II

Ze wzoru na tangens wyznaczamy sinus

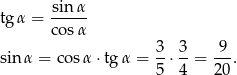
tgα = sinα- cos α 3 3 9 sinα = cosα ⋅tg α = --⋅-- = ---. 5 4 20

Liczymy sumę kwadratów sinusa i cosinusa

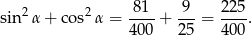
2 2 81 9 225 sin α + cos α = 40-0 + 25-= 400-.

Otrzymaliśmy sprzeczność ponieważ dla dowolnego α

sin2 α+ cos2α = 1.
Wersja PDF