/Szkoła średnia/Zadania maturalne/Matura 2008

Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 7 marca 2008 Czas pracy: 120 minut

Zadanie 1
(6 pkt)

Na rysunku jest przedstawiony wykres funkcji 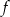f .

PIC

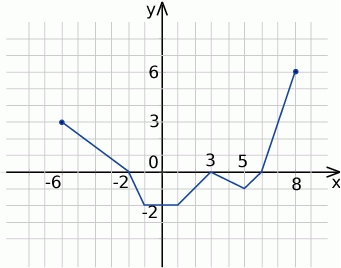
  • Podaj dziedzinę funkcji f .
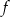  • Podaj wszystkie miejsca zerowe funkcji f .
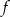  • Odczytaj wartość funkcji 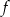f dla argumentu x = 5 .
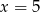  • Podaj zbiór wartości funkcji f .
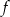  • Podaj maksymalny przedział o długości 3, w którym funkcja 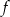f jest rosnąca.
  • Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja f przyjmuje wartości ujemne.

Zadanie 2
(5 pkt)

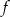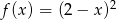Funkcja kwadratowa f jest określona wzorem f(x) = (2 − x )2 .

  • Wyznacz najmniejszą i największą wartość funkcji 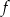f w przedziale ⟨0,5⟩ .
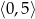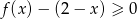  • Rozwiąż nierówność f(x) − (2 − x) ≥ 0 .

Zadanie 3
(4 pkt)

Suma dwóch liczb jest równa 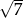√ -- 7 , a ich różnica 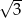√ -- 3 . Oblicz iloczyn tych liczb.

Zadanie 4
(4 pkt)

W układzie współrzędnych są dane punkty 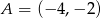A = (−4 ,−2 ) , B = (5,4) .

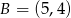  • Oblicz odległość punktu 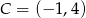C = (− 1 ,4 ) od prostej przechodzącej przez punkty 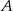A i B .
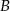  • Uzasadnij, że jeśli 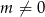m ⁄= 0 , to punkty 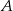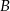A , B oraz punkt 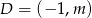D = (− 1,m ) są wierzchołkami trójkąta.

Zadanie 5
(6 pkt)

Dany jest wielomian 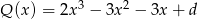Q (x) = 2x3 − 3x2 − 3x + d .

  • Liczba 1 jest pierwiastkiem tego wielomianu. Oblicz d .
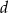  • Dla 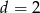d = 2 przedstaw wielomian 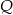Q w postaci iloczynu wielomianów stopnia pierwszego.

Zadanie 6
(4 pkt)

Rozwiąż nierówność 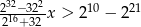32 2 2216−+3232-x > 210 − 221 . Podaj najmniejszą liczbę całkowitą spełniającą tę nierówność.

Zadanie 7
(4 pkt)

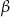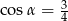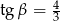Uzasadnij, że nie istnieje trójkąt prostokątny, w którym przeciwprostokątna ma długość 24, a kąty ostre α i β są takie, że cos α = 3 4 i tgβ = 4 3 .

Zadanie 8
(6 pkt)

Ciąg arytmetyczny 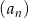(an ) jest określony wzorem 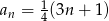an = 1(3n + 1) 4 dla n ≥ 1 .

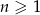  • Sprawdź, którym wyrazem ciągu 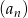(an) jest liczba 3 3 74 .
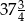  • Wśród pięćdziesięciu początkowych wyrazów ciągu 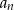an są wyrazy będące liczbami całkowitymi. Oblicz sumę wszystkich tych wyrazów.

Zadanie 9
(4 pkt)

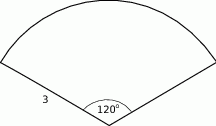
Powierzchnia boczna stożka po rozwinięciu na płaszczyznę jest wycinkiem koła o promieniu 3 i kącie środkowym 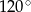120∘ (zobacz rysunek). Oblicz objętość tego stożka.

PIC

Zadanie 10
(4 pkt)

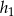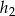W równoległoboku o obwodzie równym 144, wysokości h1 i h2 spełniają warunek 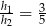h h12 = 35 . Oblicz długości boków tego równoległoboku.

Zadanie 11
(3 pkt)

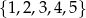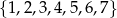Dane są zbiory liczb całkowitych: {1,2,3,4,5} i {1,2,3,4,5,6,7} . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.

Arkusz Wersja PDF
Rozwiązania