/Szkoła średnia/Zadania maturalne/Matura 2008

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 10 maja 2008 Czas pracy: 120 minut

Zadanie 1
(4 pkt)

Objętość stożka, w którym wysokość jest równa promieniowi podstawy, jest równa 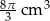8π- 3 3 cm . Oblicz pole powierzchni całkowitej tego stożka. Przyjmując przybliżenie 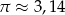π ≈ 3,14 podaj wynik z dokładnością do 0,1.

Zadanie 2
(5 pkt)

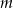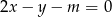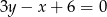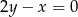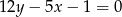Dla jakich wartości parametru m punkt przecięcia się prostych 2x − y − m = 0 i 3y − x + 6 = 0 należy do prostej 2y − x = 0 . Podaj współrzędne tego punktu i oblicz jego odległość od prostej 12y − 5x− 1 = 0 .

Zadanie 3
(5 pkt)

Stasiu wybrał się na spacer po lesie. Na wykresie przedstawiono przebytą przez niego drogę w zależności od czasu.

PIC

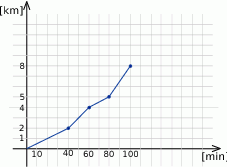
  • Oblicz z jaką średnią prędkością poruszał się w trakcie spaceru. Wynik podaj w kilometrach na godzinę.
  • W której minucie spaceru przebył dokładnie połowę drogi?
  • Z jaką największą, i z jaką najmniejszą prędkością się poruszał? Wynik podaj w kilometrach na godzinę.

Zadanie 4
(4 pkt)

Ania układa szklane kulki w figury pokazane na rysunku, na którym pokazane są pierwsze trzy figury.

PIC

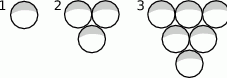
  • Niech 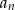an będzie różnicą liczby kulek w 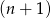(n + 1) –ej i n –tej figurze. Wypisz pierwszych 5 wyrazów ciągu (a ) n .
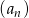  • Uzasadnij, że 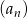(an) jest ciągiem arytmetycznym i oblicz ile potrzeba kulek do ułożenia 20 figury.

Zadanie 5
(6 pkt)

Przekątne rombu 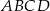ABCD , o kącie ostrym przy wierzchołku 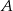A , mają długości 6cm i 8cm.

  • Oblicz cosinus kąta CAD .
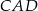  • Wyznacz promień okręgu wpisanego w romb.

Zadanie 6
(5 pkt)

Wśród 360 uczniów pewnej szkoły przeprowadzono ankietę, w której jedno z pytań brzmiało czy oglądałeś/oglądałaś wczoraj telewizję. Odpowiedzi na to pytanie są przedstawione na wykresach poniżej.

PIC

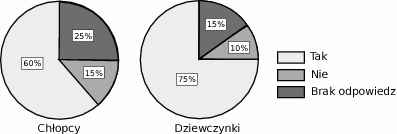
Wiedząc, że dziewczęta stanowią 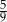59 ankietowanych osób odpowiedz na pytania.

  • Ile sposród ankietowanych osób nie odpowiedziało na zadane pytanie?
  • Jaki procent ankietowanych osób oglądało wczoraj telewizję? Wynik podaj z dokładnością do 1%.
  • Jaki procent chłopców, spośród tych, którzy udzielili odpowiedzi na pytanie, nie oglądało wczoraj telewizji?

Zadanie 7
(4 pkt)

Rozwiąż nierówność

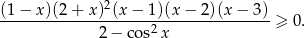
2 (1-−-x)(2-+-x-)(x-−-1-)(x−--2)(x−--3) ≥ 0. 2− cos2x

Zadanie 8
(5 pkt)

W pewnej klasie okazało się, że są 3 osoby, które urodziły się w kwietniu tego samego roku i są dwie osoby, które urodziły się w lipcu tego samego roku. Oblicz prawdopodobieństwo, że troje z tych 5 uczniów urodziło się tego samego dnia roku.

Zadanie 9
(3 pkt)

W ciągu geometrycznym 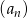(an) , którego żaden wyraz nie jest równy 0, suma pewnych dwóch kolejnych wyrazów jest równa 0. Oblicz sumę 2008 początkowych wyrazów tego ciągu.

Zadanie 10
(4 pkt)

Rozwiąż równanie 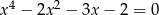4 2 x − 2x − 3x − 2 = 0 .

Zadanie 11
(5 pkt)

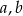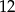O liczbach a,b i c wiadomo, że tworzą ciąg arytmetyczny oraz ich suma wynosi 12 . Wyznacz największą możliwą wartość wyrażenia 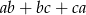ab + bc + ca . Dla jakich liczb 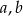a,b i c wartość ta jest osiągana.

Arkusz Wersja PDF
Rozwiązania