/Szkoła średnia/Zadania maturalne/Matura 2010/Materiały pomocnicze
Zbiór zadań maturalnych
z Matematyki Matura 2010
poziom podstawowy Informator CKE Część 2: zadania otwarte
Zadania krótkiej odpowiedzi
Rozwiąż równanie 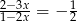 .
.
Rozwiąż układ równań 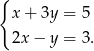
Rozwiąż nierówność 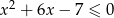 .
.
Rozwiąż równanie  .
.
O funkcji liniowej 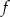 wiadomo, że
wiadomo, że 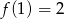 oraz, że do wykresu tej funkcji należy punkt
oraz, że do wykresu tej funkcji należy punkt 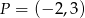 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 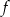 .
.
Oblicz miejsca zerowe funkcji
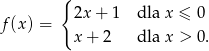
Naszkicuj wykres funkcji
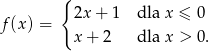
Oblicz najmniejszą wartość funkcji kwadratowej 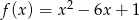 w przedziale
w przedziale 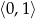 .
.
Wielomiany 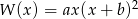 i
i 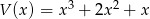 są równe. Oblicz
są równe. Oblicz  i
i 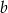 .
.
Wyrażenie 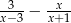 zapisz w postaci ilorazu dwóch wielomianów.
zapisz w postaci ilorazu dwóch wielomianów.
Napisz równanie prostej równoległej do prostej o równaniu 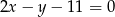 i przechodzącej przez punkt
i przechodzącej przez punkt 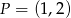 .
.
Wyznacz równanie okręgu stycznego do osi 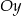 , którego środkiem jest punkt
, którego środkiem jest punkt 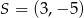 .
.
Wyznacz równanie okręgu o środku 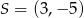 przechodzącego przez początek układu współrzędnych.
przechodzącego przez początek układu współrzędnych.
Wyznacz równanie prostej zawierającej środkową 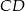 trójkąta
trójkąta 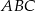 , którego wierzchołkami są punkty:
, którego wierzchołkami są punkty: 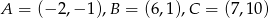 .
.
W trójkącie prostokątnym, w którym przyprostokątne mają długości 2 i 4, jeden z kątów ostrych ma miarę  . Oblicz
. Oblicz 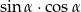 .
.
Kąt  jest ostry i
jest ostry i 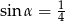 . Oblicz
. Oblicz 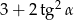 .
.
Punkt 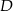 leży na boku
leży na boku 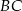 trójkąta równoramiennego
trójkąta równoramiennego 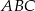 , w którym
, w którym 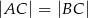 .
.
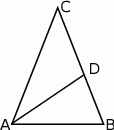
Odcinek 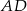 dzieli trójkąt
dzieli trójkąt 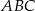 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 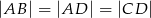 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 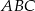 .
.
Oblicz pole trójkąta równoramiennego 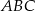 , w którym
, w którym 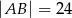 i
i 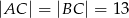 .
.
Liczby 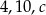 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 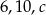 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Liczby 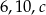 są długościami boków trójkąta prostokątnego. Oblicz
są długościami boków trójkąta prostokątnego. Oblicz  .
.
Liczby 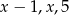 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Obwód czworokąta wypukłego 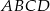 jest równy 50 cm. Obwód trójkąta
jest równy 50 cm. Obwód trójkąta 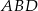 jest równy 46 cm, a obwód trójkąta
jest równy 46 cm, a obwód trójkąta 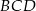 jest równy 36 cm. Oblicz długość przekątnej
jest równy 36 cm. Oblicz długość przekątnej 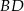 .
.
Ile wyrazów ujemnych ma ciąg 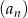 określony wzorem
określony wzorem 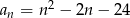 dla
dla 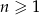 ?
?
Liczby 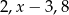 są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz
są w podanej kolejności pierwszym, drugim i czwartym wyrazem ciągu arytmetycznego. Oblicz  .
.
Wyrazami ciągu arytmetycznego 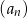 są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto
są kolejne liczby naturalne, które przy dzieleniu przez 5 dają resztę 2. Ponadto 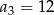 . Oblicz
. Oblicz 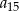 .
.
Ile jest liczb naturalnych czterocyfrowych takich, że w ich zapisie dziesiętnym występuje jedna cyfra nieparzysta i trzy cyfry parzyste?
Uwaga: przypominamy, że zero jest liczbą parzystą.
Ile jest liczb naturalnych dwucyfrowych podzielnych przez 15 lub 20?
Ile jest liczb naturalnych trzycyfrowych, w których cyfra dziesiątek jest o 2 większa od cyfry jedności?
Na jednej prostej zaznaczono 3 punkty, a na drugiej 4 punkty.
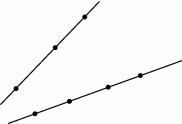
Ile jest wszystkich trójkątów, których wierzchołkami są trzy spośród zaznaczonych punktów?
Średnia arytmetyczna liczb: 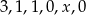 jest równa 2. Oblicz
jest równa 2. Oblicz  .
.
Oblicz średnią arytmetyczną danych przedstawionych na poniższym diagramie częstości
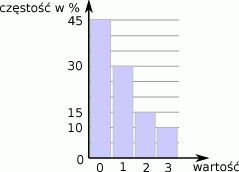
Oblicz medianę danych: 0, 1, 3, 3, 1, 1, 2, 1.
Oblicz medianę danych przedstawionych w postaci tabeli liczebności
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 4 | 3 | 1 | 1 |
Ze zbioru liczb 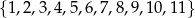 wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 3 lub przez 2.
wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 3 lub przez 2.
Ze zbioru liczb naturalnych dwucyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 5.
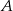 i
i 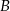 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 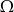 , że
, że 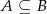 oraz
oraz 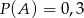 i
i 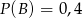 . Oblicz prawdopodobieństwo
. Oblicz prawdopodobieństwo 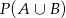 .
.
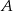 i
i 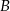 są takimi zdarzeniami losowymi zawartymi w
są takimi zdarzeniami losowymi zawartymi w 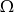 , że
, że 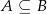 oraz
oraz 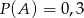 i
i 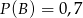 . Oblicz prawdopodobieństwo różnicy
. Oblicz prawdopodobieństwo różnicy 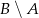 .
.
Przekątna sześcianu ma długość 9. Oblicz pole powierzchni całkowitej tego sześcianu.
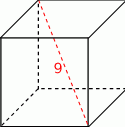
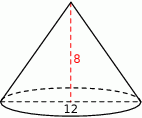
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
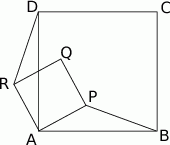
Czworokąty 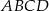 i
i 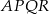 są kwadratami. Udowodnij, że
są kwadratami. Udowodnij, że 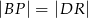 .
.
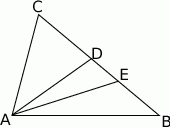
Na boku 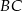 trójkąta
trójkąta 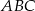 wybrano punkt
wybrano punkt 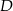 tak, by
tak, by 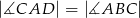 . Odcinek
. Odcinek 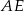 jest dwusieczną kąta
jest dwusieczną kąta 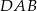 . Udowodnij, że
. Udowodnij, że 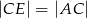 .
.
Zadania rozszerzonej odpowiedzi
Oblicz sumę wszystkich liczb trzycyfrowych zapisanych wyłącznie za pomocą cyfr wybranych ze zbioru 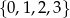 .
.
Z pojemnika, w którym są dwa losy wygrywające i trzy losy puste, losujemy dwa razy po jednym losie bez zwracania. Oblicz prawdopodobieństwo, że otrzymamy co najmniej jeden los wygrywający. Wynik przedstaw w postaci ułamka nieskracalnego.
Z miejscowości 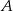 i
i 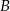 oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości
oddalonych od siebie o 182 km wyjeżdżają naprzeciw siebie dwaj rowerzyści. Rowerzysta jadący z miejscowości 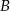 do miejscowości
do miejscowości 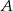 jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości
jedzie ze średnią prędkością mniejszą od 25 km/h. Rowerzysta jadący z miejscowości 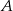 do miejscowości
do miejscowości 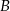 wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości
wyjeżdża o 1 godzinę wcześniej i jedzie ze średnią prędkością o 7 km/h większą od średniej prędkości drugiego rowerzysty. Rowerzyści spotkali się w takim miejscu, że rowerzysta jadący z miejscowości 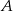 przebył do tego miejsca
przebył do tego miejsca 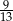 całej drogi z
całej drogi z 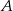 do
do 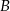 . Z jakimi średnimi prędkościami jechali obaj rowerzyści?
. Z jakimi średnimi prędkościami jechali obaj rowerzyści?
Uczeń przeczytał książkę liczącą 480 stron, przy czym każdego dnia czytał taką samą liczbę stron. Gdyby czytał każdego dnia o 8 stron więcej to przeczytałby tę książkę o 3 dni wcześniej. Ile dni czytał tę książkę?
Trzy liczby, których suma jest równa 93, tworzą ciąg geometryczny. Te same liczby stanowią pierwszy, drugi oraz siódmy wyraz ciągu arytmetycznego. Wyznacz te liczby.
Wyznacz wzór na  -ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
-ty wyraz ciągu arytmetycznego wiedząc, że suma pierwszych pięciu jego wyrazów jest równa 10, a wyrazy trzeci, piąty i trzynasty tworzą w podanej kolejności ciąg geometryczny.
Podstawą ostrosłupa prawidłowego czworokątnego 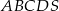 jest kwadrat
jest kwadrat 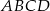 . Pole trójkąta równoramiennego
. Pole trójkąta równoramiennego 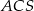 jest równe 120 oraz
jest równe 120 oraz 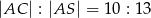 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
Podstawą ostrosłupa 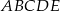 jest kwadrat
jest kwadrat 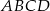 . Punkt
. Punkt 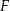 jest środkiem krawędzi
jest środkiem krawędzi 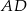 , odcinek
, odcinek 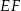 jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że
jest wysokością ostrosłupa. Oblicz objętość ostrosłupa, jeśli wiadomo, że 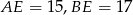 .
.
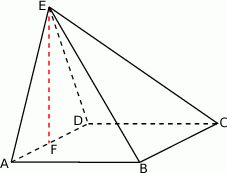
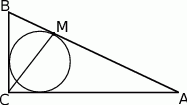
Dany jest trójkąt prostokątny 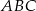 , w którym
, w którym 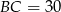 ,
, 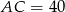 i
i 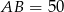 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 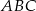 jest styczny do boku
jest styczny do boku 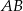 w punkcie
w punkcie 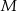 . Oblicz długość odcinka
. Oblicz długość odcinka 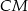 .
.
Na zewnątrz trójkąta prostokątnego 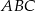 , w którym
, w którym 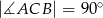 oraz
oraz 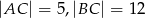 zbudowano kwadrat
zbudowano kwadrat 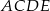 .
.
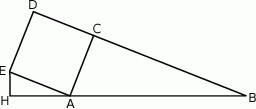
Punkt 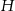 leży na prostej
leży na prostej 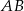 i kąt
i kąt 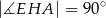 . Oblicz pole trójkąta
. Oblicz pole trójkąta 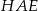 .
.
Wykaż, że prawdziwa jest nierówność 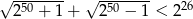 .
.
Udowodnij, że jeśli
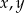 są liczbami rzeczywistymi, to
są liczbami rzeczywistymi, to 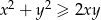 .
. 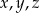 są liczbami rzeczywistymi takimi, że
są liczbami rzeczywistymi takimi, że 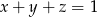 , to
, to 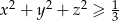 .
.
Punkt 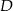 leży na boku
leży na boku 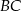 trójkąta równoramiennego
trójkąta równoramiennego 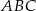 , w którym
, w którym 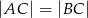 .
.
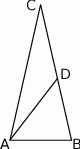
Odcinek 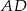 dzieli trójkąt
dzieli trójkąt 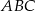 na dwa trójkąty równoramienne w taki sposób, że
na dwa trójkąty równoramienne w taki sposób, że 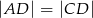 oraz
oraz 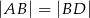 . Udowodnij, że
. Udowodnij, że 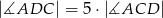 .
.
Dane są dwa półokręgi o wspólnym środku 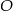 i średnicach odpowiednio
i średnicach odpowiednio 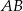 i
i 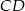 (punkty
(punkty 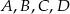 i
i 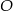 są współliniowe).
są współliniowe).
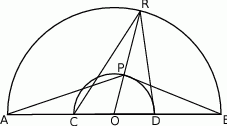
Punkt 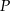 leży na wewnętrznym półokręgu, punkt
leży na wewnętrznym półokręgu, punkt 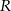 leży na zewnętrznym półokręgu, punkty
leży na zewnętrznym półokręgu, punkty 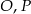 i
i 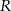 są współliniowe. Udowodnij, że
są współliniowe. Udowodnij, że 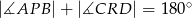 .
.

