/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna
Próbny Egzamin Maturalny
z Matematyki poziom podstawowy 3 listopada 2009 Czas pracy: 170 minut
Zadania zamknięte
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 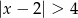 B)
B) 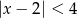 C)
C) 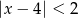 D)
D) 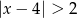
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 33% C) 45% D) 63%
6% liczby  jest równe 9. Wtedy
jest równe 9. Wtedy
A) 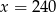 B)
B) 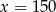 C)
C) 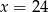 D)
D) 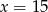
Iloraz 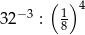
A) 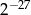 B)
B) 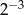 C)
C) 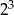 D)
D) 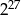
O liczbie  wiadomo, że
wiadomo, że 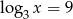 . Zatem
. Zatem
A) 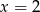 B)
B) 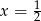 C)
C) 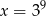 D)
D) 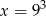
Wyrażenie 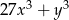 jest równe iloczynowi
jest równe iloczynowi
A) 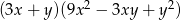
B) 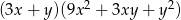
C) 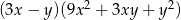
D) 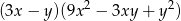
Dane są wielomiany 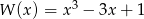 oraz
oraz 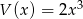 . Wielomian
. Wielomian 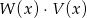 jest równy
jest równy
A) 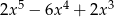 B)
B) 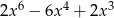 C)
C) 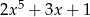 D)
D) 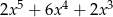
Wierzchołek paraboli o równaniu 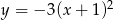 ma współrzędne
ma współrzędne
A) 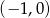 B)
B) 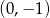 C)
C) 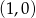 D)
D) 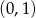
Do wykresu funkcji 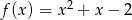 należy punkt
należy punkt
A) 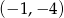 B)
B) 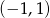 C)
C) 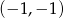 D)
D) 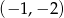
Rozwiązaniem równania 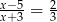 jest liczba
jest liczba
A) 21 B) 7 C) 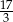 D) 0
D) 0
Zbiór rozwiązań nierówności 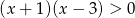 przedstawiony jest na rysunku
przedstawiony jest na rysunku
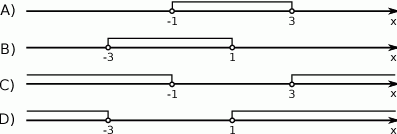
Dla 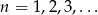 ciąg
ciąg 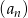 jest określony wzorem
jest określony wzorem 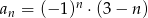 . Wtedy
. Wtedy
A) 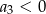 B)
B) 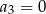 C)
C) 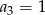 D)
D) 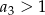
W ciągu arytmetycznym trzeci wyraz jest równy 14, a jedenasty jest równy 34. Różnica tego ciągu jest równa
A) 9 B)  C) 2 D)
C) 2 D) 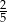
W ciągu geometrycznym 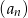 dane są:
dane są: 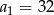 i
i 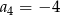 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 12 B) 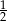 C)
C) 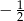 D) -12
D) -12
Kąt  jest ostry i
jest ostry i 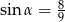 . Wówczas
. Wówczas 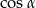 jest równy
jest równy
A) 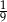 B)
B) 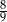 C)
C) 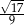 D)
D) 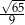
Dany jest trójkąt prostokątny (patrz rysunek).
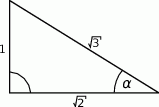
Wtedy 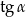 jest równy
jest równy
A) 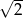 B)
B) 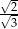 C)
C) 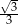 D)
D) 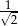
W trójkącie równoramiennym 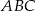 dane są
dane są 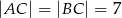 oraz
oraz 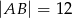 . Wysokość opuszczona z wierzchołka
. Wysokość opuszczona z wierzchołka 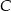 jest równa
jest równa
A) 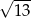 B)
B) 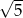 C) 1 D) 5
C) 1 D) 5
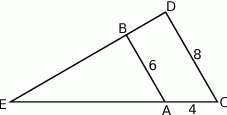
Oblicz długość odcinka 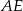 wiedząc, że
wiedząc, że 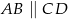 i
i 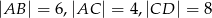 .
.
A) 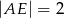 B)
B) 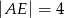 C)
C) 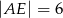 D)
D) 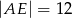
Dane są punkty 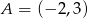 oraz
oraz 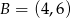 . Długość odcinka
. Długość odcinka 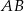 jest równa
jest równa
A) 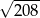 B)
B) 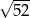 C)
C) 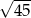 D)
D) 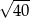
Promień okręgu o równaniu 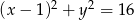 jest równy
jest równy
A) 1 B) 2 C) 3 D) 4
Wykres funkcji liniowej określonej wzorem 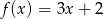 jest prostą prostopadłą do prostej o równaniu:
jest prostą prostopadłą do prostej o równaniu:
A) 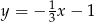 B)
B) 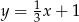 C)
C) 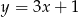 D)
D) 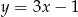
Prosta o równaniu 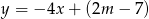 przechodzi przez punkt
przechodzi przez punkt 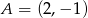 . Wtedy
. Wtedy
A) 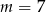 B)
B) 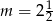 C)
C) 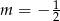 D)
D) 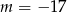
Pole powierzchni całkowitej sześcianu jest równe 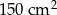 . Długość krawędzi tego sześcianu jest równa
. Długość krawędzi tego sześcianu jest równa
A) 3,5 cm B) 4 cm C) 4,5 cm D) 5 cm
Średnia arytmetyczna pięciu liczb: 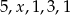 jest równa 3. Wtedy
jest równa 3. Wtedy
A) 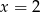 B)
B) 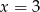 C)
C) 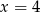 D)
D) 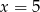
Wybieramy liczbę  ze zbioru
ze zbioru 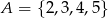 oraz liczbę
oraz liczbę 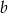 ze zbioru
ze zbioru 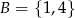 . Ile jest takich par
. Ile jest takich par 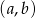 , że iloczyn
, że iloczyn 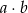 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 2 B) 3 C) 5 D) 20
Zadania otwarte
Rozwiąż nierówność 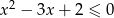 .
.
Rozwiąż równanie 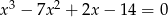 .
.
W układzie współrzędnych na płaszczyźnie punkty 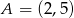 i
i 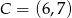 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 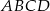 . Wyznacz równanie prostej
. Wyznacz równanie prostej 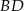 .
.
Kąt  jest ostry oraz
jest ostry oraz 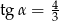 . Oblicz
. Oblicz 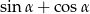 .
.
Wykaż, że dla każdego 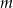 ciąg
ciąg 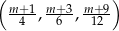 jest arytmetyczny.
jest arytmetyczny.
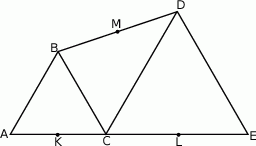
Trójkąty 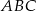 i
i 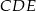 są równoboczne. Punkty
są równoboczne. Punkty 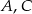 i
i 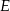 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 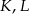 i
i 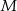 są środkami odcinków
są środkami odcinków 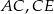 i
i 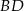 (zobacz rysunek). Wykaż, że punkty
(zobacz rysunek). Wykaż, że punkty 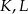 i
i  są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
Uczeń przeczytał książkę liczącą 480 stron, przy czym każdego dnia czytał taką samą liczbę stron. Gdyby czytał każdego dnia o 8 stron więcej to przeczytałby tę książkę o 3 dni wcześniej. Ile dni czytał tę książkę?
Punkty 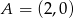 i
i 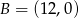 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 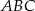 o przeciwprostokątnej
o przeciwprostokątnej 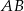 . Wierzchołek
. Wierzchołek 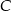 leży na prostej o równaniu
leży na prostej o równaniu 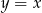 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 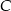 .
.
Pole trójkąta prostokątnego jest równe 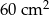 . Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.
. Jedna przyprostokątna jest o 7 cm dłuższa od drugiej. Oblicz długość przeciwprostokątnej tego trójkąta.

