/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 17 kwietnia 2010 Czas pracy: 170 minut
Zadania zamknięte
Jeżeli liczba 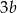 jest o 20% większa od połowy liczby
jest o 20% większa od połowy liczby 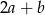 , to liczba
, to liczba  jest większa od
jest większa od 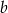 o
o
A) 100% B) 80% C) 50% D) 200%
Stosunek miar kątów czworokąta jest równy 6:7:8:9. Najmniejszy kąt tego czworokąta ma miarę
A) 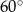 B)
B) 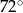 C)
C) 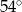 D)
D) 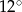
Połową odwrotności sześcianu liczby 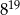 jest
jest
A) 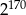 B)
B) 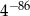 C)
C) 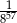 D)
D) 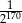
Wartość wielomianu 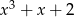 dla argumentu
dla argumentu 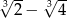 jest równa
jest równa
A) 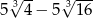 B)
B) 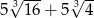 C)
C) 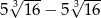 D)
D) 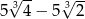
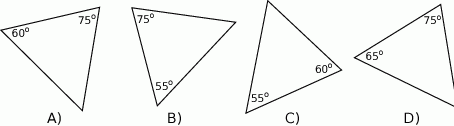
Który z narysowanych trójkątów jest podobny do trójkąta, w którym miary dwóch kątów wynoszą 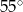 i
i 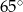 ?
?
Wskaż zbiór, w którym funkcja 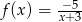 jest rosnąca.
jest rosnąca.
A) 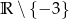 B)
B) 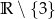 C)
C) 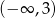 D)
D) 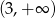
Które z poniższych zdań nie jest prawdziwe?
A) Na każdym prostokącie można opisać okrąg.
B) W każdy romb można wpisać okrąg.
C) Na każdym równoległoboku można opisać okrąg.
D) W każdy deltoid można wpisać okrąg.
Zbiorem wartości funkcji kwadratowej 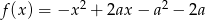 jest przedział
jest przedział 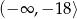 . Zatem
. Zatem
A) 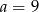 B)
B) 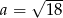 C)
C) 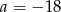 D)
D) 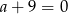
Wartość wyrażenia 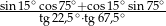 jest równa
jest równa
A) 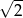 B)
B) 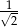 C) 1 D)
C) 1 D) 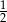
Która z liczb jest równa liczbie 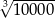 ?
?
A) 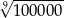 B)
B) 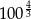 C)
C) 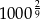 D)
D) 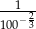
Bok 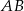 czworokąta
czworokąta 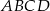 wpisanego w okrąg jest średnicą okręgu oraz
wpisanego w okrąg jest średnicą okręgu oraz 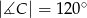 .
.
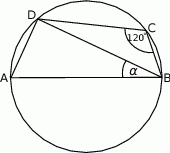
Zatem kąt  ma miarę
ma miarę
A) 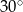 B)
B) 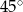 C)
C) 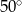 D)
D) 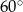
Rozwiązaniem równania 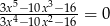 jest liczba
jest liczba
A) 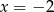 B)
B) 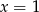 C)
C) 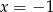 D)
D) 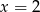
Liczba 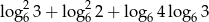 jest
jest
A) dodatnia B) mniejsza od 1 C) ujemna D) niewymierna
Suma  początkowych wyrazów ciągu arytmetycznego
początkowych wyrazów ciągu arytmetycznego 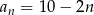 , gdzie
, gdzie 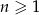 jest równa 14. Zatem
jest równa 14. Zatem
A) 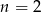 B) liczba
B) liczba 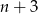 dzieli się przez 5 C)
dzieli się przez 5 C) 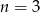 D)
D) 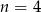
Wykres funkcji 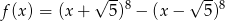 przecina oś
przecina oś 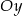 w punkcie
w punkcie
A) 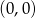 B)
B) 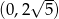 C)
C) 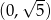 D)
D) 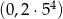
Punkt 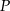 jest punktem wspólnym środkowych
jest punktem wspólnym środkowych 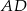 i
i 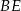 w trójkącie
w trójkącie 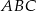 . Wówczas odcinki
. Wówczas odcinki 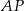 i
i 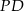 mogą mieć długości
mogą mieć długości
A) 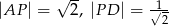
B) 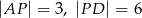
C) 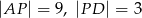
D) 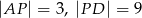
Pięć spośród sześciu różnokolorowych kul wkładamy do pięciu ponumerowanych szuflad tak, że w każdej szufladzie znajduje się jedna kula. Na ile różnych sposobów można to zrobić?
A) 120 B) 720 C) 24 D) 126
Równanie prostej przechodzącej przez punkty 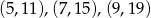 to
to
A) 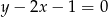 B)
B) 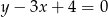 C)
C) 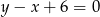 D)
D) 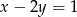
Krawędź podstawy ostrosłupa prawidłowego czworokątnego jest dwa razy dłuższa od jego wysokości. Kąt nachylenia ściany bocznej do podstawy ma miarę
A) 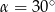 B)
B) 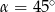 C)
C) 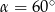 D)
D) 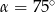
Diagram przedstawia ile procent rodzin mieszkających w jednym z łódzkich bloków posiada 0,1,2,3 lub 4 dzieci.
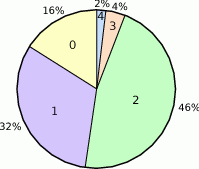
Średnia liczba dzieci przypadających na jedną rodzinę jest równa
A) 1,22 B) 1,44 C) 2 D) 2,5
Warunek „przynajmniej jedna z liczb 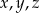 jest niezerowa” jest równoważny warunkowi
jest niezerowa” jest równoważny warunkowi
A) 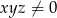
B) 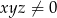 oraz
oraz 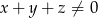
C) 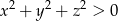
D) 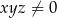 oraz
oraz 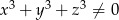
Układ równań 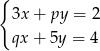 z niewiadomymi
z niewiadomymi  i
i 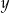 ma nieskończenie wiele rozwiązań. Zatem liczba
ma nieskończenie wiele rozwiązań. Zatem liczba 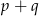 jest równa
jest równa
A) 6 B) 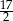 C)
C) 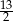 D) 15
D) 15
Zadania otwarte
Wykaż, że dla każdej liczby naturalnej  , liczby
, liczby 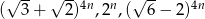 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Wyznacz dziedzinę funkcji 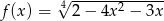 .
.
Oblicz pole kwadratu wiedząc, że różnica pól kół opisanego i wpisanego w ten kwadrat jest równa 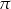 .
.
Wyznacz współrzędne wierzchołka 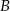 równoległoboku
równoległoboku 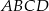 jeżeli
jeżeli 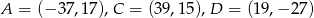 .
.
Rozwiąż nierówność 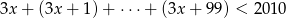 , gdzie lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
, gdzie lewa strona jest sumą kolejnych wyrazów ciągu arytmetycznego.
Punkt 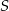 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 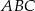 . Wykaż, że jeżeli
. Wykaż, że jeżeli 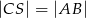 to
to 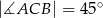 .
.
Przy jednoczesnej pracy 40 identycznych pomp nadmuchowych, żądany przepływ powietrza można zrealizować w ciągu 24 godzin. W ciągu ilu godzin można zrealizować ten sam przepływ powietrza przy jednoczesnej pracy 60 pomp?
Dany jest wykres funkcji 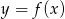 określonej dla
określonej dla 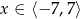 .
.
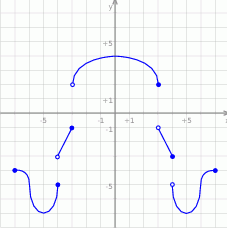
Odczytaj z wykresu:
- rozwiązania równania
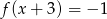 ;
; - miejsca zerowe funkcji
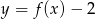 ;
; - maksymalne przedziały monotoniczności funkcji
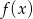 .
.
Na prostej 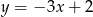 wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
wyznacz punkt, którego suma kwadratów odległości od osi układu współrzędnych jest najmniejsza.
Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobieństwo, że przynajmniej dwa listy znajdą się w tej samej skrzynce?

