/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy 6 marca 2010 Czas pracy: 170 minut
Zadania zamknięte
Liczba 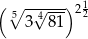 jest równa
jest równa
A) 3 B) 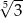 C)
C) 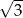 D) 9
D) 9
Ile liczb całkowitych spełnia nierówność 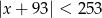 ?
?
A) 504 B) 505 C) 506 D) 507
W solance, która zawierała 8% soli zwiększono zawartość soli o 187,5%. Stężenie soli w otrzymanym roztworze wynosi
A) 23% B) 20% C) 18% D) 25%
Jeżeli 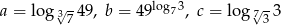 to
to
A) 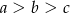 B)
B) 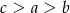 C)
C) 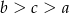 D)
D) 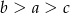
Równanie 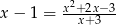
A) spełnia każda liczba rzeczywista
B) jest sprzeczne
C) ma mniej niż 5 rozwiązań
D) ma rozwiązania ujemne
Wskaż wzór funkcji, która przecina osie układu współrzędnych w 3 punktach.
A) 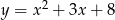
B) 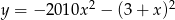
C) 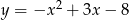
D) 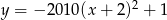
Suma kwadratów trzech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 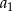 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 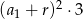 B)
B) 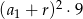 C)
C) 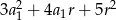 D)
D) 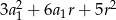
W trójkącie 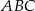 poprowadzono odcinek
poprowadzono odcinek 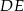 równoległy do boku
równoległy do boku 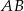 w ten sposób, że
w ten sposób, że 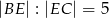 .
.
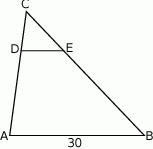
Jeżeli 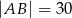 to długość odcinka
to długość odcinka 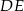 jest równa
jest równa
A) 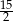 B) 6 C) 5 D)
B) 6 C) 5 D) 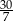
Wyrażenie 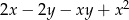 jest równe wyrażeniu
jest równe wyrażeniu
A) 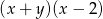 B)
B) 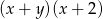 C)
C) 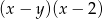 D)
D) 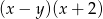
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 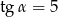 . Zatem
. Zatem
A) 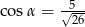 B)
B) 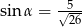 C)
C) 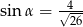 D)
D) 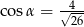
Jeżeli wykres funkcji 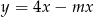 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 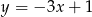 to
to
A) 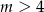 B)
B) 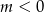 C)
C) 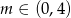 D)
D) 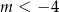
Na pierwszym polu 64-polowej szachownicy kładziemy jedno ziarnko maku, na drugim dwa ziarnka maku, na trzecim dwa razy więcej niż na drugim, na czwartym dwa razy więcej niż na trzecim itd. Ile ziarenek maku położymy w sumie na szachownicy?
A) 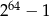 B)
B) 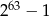 C)
C) 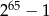 D)
D) 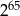
Dziedziną funkcji 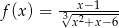 jest zbiór
jest zbiór
A) 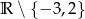 B)
B) 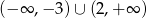 C)
C) 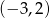 D)
D) 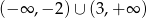
W kwadracie  połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat  .
.
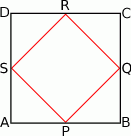
Kwadrat 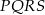 jest podobny do kwadratu
jest podobny do kwadratu 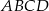 w skali
w skali
A) 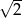 B) 2 C)
B) 2 C) 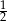 D)
D) 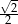
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 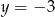 i okręgu
i okręgu 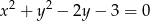 ?
?
A) 1 B) 2 C) 3 D) 4
Przedstawiony na rysunku wykres może być wykresem funkcji
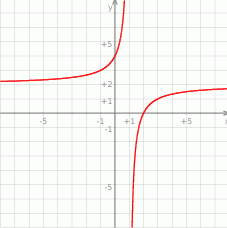
A) 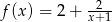 B)
B) 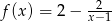 C)
C) 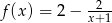 D)
D) 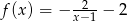
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 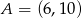 i
i 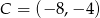 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 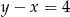 B)
B) 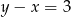 C)
C) 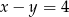 D)
D) 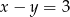
Losujemy jedną liczbę trzycyfrową. Prawdopodobieństwo 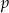 otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
A) 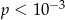 B)
B) 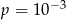 C)
C) 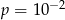 D)
D) 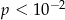
Liczby naturalne 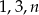 są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
są długościami boków trójkąta. Połowa obwodu tego trójkąta jest równa
A) 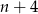 B)
B) 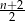 C)
C) 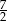 D) 3
D) 3
Objętość kuli stycznej do wszystkich ścian sześcianu o krawędzi długości 6 jest równa
A)  B)
B) 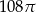 C)
C) 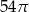 D)
D) 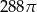
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.
![]()
A) 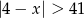 B)
B) 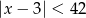 C)
C) 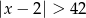 D)
D) 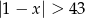
Zadania otwarte
Dwaj rowerzyści pokonują trasę między punktami 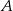 i
i 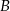 . O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?
. O ile procent średnia prędkość drugiego rowerzysty musi być większa od średniej prędkości pierwszego rowerzysty, aby przyjechał on o 20% szybciej?
Boki prostokąta 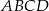 mają długości 5 i 12. Oblicz odległość wierzchołka
mają długości 5 i 12. Oblicz odległość wierzchołka 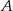 od przekątnej
od przekątnej 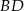 .
.
Oblicz ile liczb podzielnych przez 7 znajduje się w przedziale 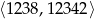 .
.
Oblicz 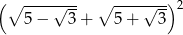 .
.
W trójkącie 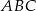 , w którym
, w którym 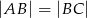 połączono wierzchołek
połączono wierzchołek 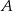 punktem
punktem 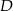 na boku
na boku 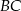 w ten sposób, że
w ten sposób, że 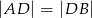 . Wyznacz miary kątów trójkąta
. Wyznacz miary kątów trójkąta 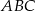 jeżeli
jeżeli 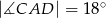 .
.
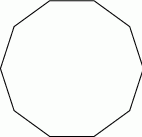
Ile można utworzyć trójkątów równoramiennych, których wierzchołki są jednocześnie wierzchołkami ustalonego dziesięciokąta foremnego?
Udowodnij, że jeżeli 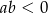 to
to 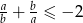 .
.
Na wykresie przedstawiono fragment wykresu wielomianu 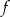 stopnia 3.
stopnia 3.
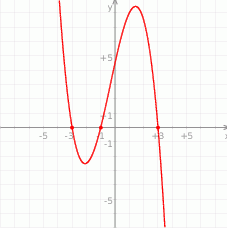
Widząc, że 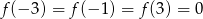 oraz
oraz 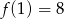 wykaż, że
wykaż, że 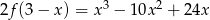 .
.
Z murów zamku wystrzelono pocisk armatni, który po 4 sekundach spadł na ziemię. Wysokość (w metrach), na jaką wzniósł się pocisk (względem poziomu armaty) po upływie 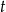 sekund od momentu wystrzelenia opisuje funkcja
sekund od momentu wystrzelenia opisuje funkcja 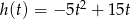 , gdzie
, gdzie 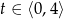 .
.
- Oblicz po jakim czasie pocisk ponownie znalazł się na wysokości z jakiej został wystrzelony.
- Oblicz na jaką maksymalną wysokość względem ziemi wzniósł się ten pocisk.
Oblicz objętość graniastosłupa prawidłowego trójkątnego, w którym krawędź podstawy ma długość 1, a przekątna ściany bocznej tworzy z sąsiednią ścianą kąt o mierze 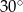 .
.

