Zadanie nr 3099471
Oblicz pole pięciokąta 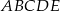 , którego wierzchołki mają współrzędne
, którego wierzchołki mają współrzędne 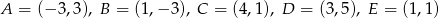 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
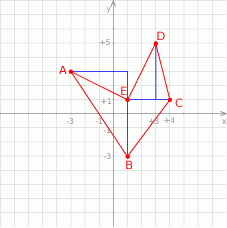
Zauważmy, że interesujący nas pięciokąt składa się z trzech trójkątów: 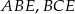 i
i 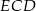 , których pola jest dość łatwo obliczyć.
, których pola jest dość łatwo obliczyć.
Trójkąty 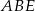 i
i 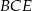 mają wspólną podstawę
mają wspólną podstawę 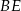 , która ma długość
, która ma długość

Wysokość trójkąta 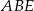 jest równa
jest równa
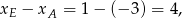
a wysokość trójkąta 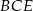 jest równa
jest równa
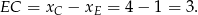
Zatem pola tych trójkątów są równe
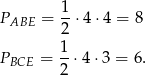
Pozostało policzyć pole trójkąta 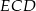 . Wiemy już, że
. Wiemy już, że 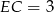 , a wysokość opuszczona na tę podstawę jest równa
, a wysokość opuszczona na tę podstawę jest równa
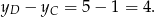
Zatem
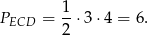
Stąd
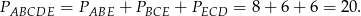
Odpowiedź: 20

