Zadanie nr 6551912
Która z poniższych funkcji nie ma minimum lokalnego ani maksimum lokalnego?
A) 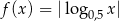 B)
B) 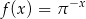 C)
C) 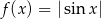 D)
D) 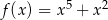
Rozwiązanie
Wykresy funkcji 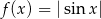 i
i 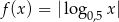 powstają z wykresów
powstają z wykresów 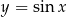 i
i 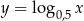 przez odbicie części wykresu znajdującego się poniżej osi
przez odbicie części wykresu znajdującego się poniżej osi 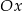 do góry.
do góry.
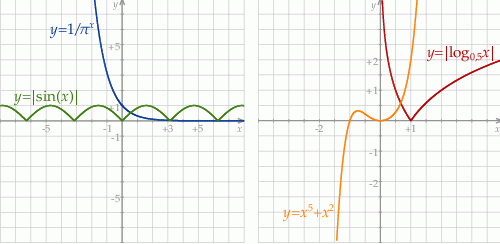
Jeżeli naszkicujemy te wykresy, to jest jasne, że obie te funkcje mają minima lokalne (pierwsza ma nieskończenie maksimów i minimów, a druga ma minimum lokalne w 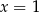 ).
).
Pochodna funkcji 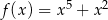 jest równa
jest równa
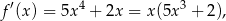
więc widać, że funkcja ta ma minimum lokalne w 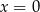 .
.
Ponieważ 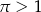 funkcja
funkcja 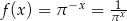 jest funkcją malejącą – nie ma więc ekstremów lokalnych.
jest funkcją malejącą – nie ma więc ekstremów lokalnych.
Odpowiedź: B

